Perbezaan antara FFT dan DFT

Fast Fourier Transform (FFT) vs. Transformasi Fourier Diskret (DFT)

Teknologi dan sains berjalan lancar. Dan tidak ada contoh yang lebih baik daripada pemprosesan isyarat digital ini (DSP). Pemprosesan isyarat digital adalah proses untuk mengoptimumkan ketepatan dan kecekapan komunikasi digital. Segala -galanya adalah data - sama ada imej dari probe luar angkasa atau getaran seismik dan apa sahaja di antara. Untuk menukar data ini ke dalam format yang boleh dibaca manusia menggunakan komputer adalah pemprosesan isyarat digital. Ini adalah salah satu teknologi paling kuat yang menggabungkan teori matematik dan pelaksanaan fizikal. Kajian DSP bermula sebagai kursus peringkat siswazah dalam kejuruteraan elektrik, tetapi dari masa ke masa, ia telah menjadi gamechanger yang berpotensi dalam bidang sains dan kejuruteraan. Cukup untuk mengatakan, tanpa DSP, jurutera dan saintis mungkin berhenti wujud.

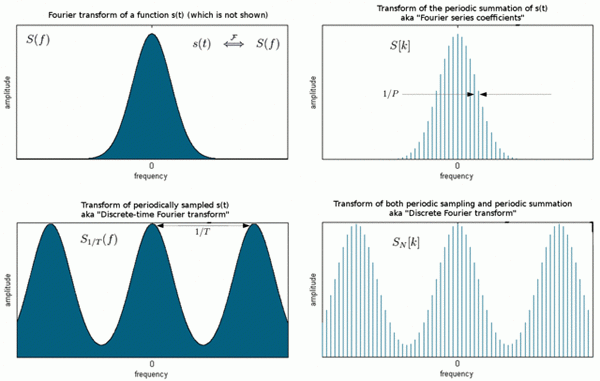
Transformasi Fourier adalah cara pemetaan isyarat, dalam domain masa atau ruang ke spektrumnya dalam domain frekuensi. Domain masa dan kekerapan hanyalah cara alternatif untuk mewakili isyarat dan transformasi Fourier adalah hubungan matematik antara kedua -dua representasi. Perubahan isyarat dalam satu domain juga akan menjejaskan isyarat dalam domain lain, tetapi tidak semestinya dengan cara yang sama. Transformasi Fourier Diskret (DFT) adalah transformasi seperti transformasi Fourier yang digunakan dengan isyarat digital. Seperti namanya, ia adalah versi diskret FT yang melihat kedua -dua domain masa dan domain kekerapan sebagai berkala. Fast Fourier Transform (FFT) hanyalah algoritma untuk pengiraan cepat dan cekap DFT.

Transformasi Fourier Diskret (DFT)

Transformasi Fourier Diskret (DFT) adalah salah satu alat yang paling penting dalam pemprosesan isyarat digital yang mengira spektrum isyarat jangka panjang. Sangat biasa untuk menyandikan maklumat dalam sinusoid yang membentuk isyarat. Walau bagaimanapun, dalam beberapa aplikasi, bentuk bentuk gelombang domain masa bukan aplikasi untuk isyarat di mana kandungan frekuensi isyarat menjadi sangat berguna dalam cara selain daripada isyarat digital. Perwakilan isyarat digital dari segi komponen kekerapannya dalam domain frekuensi adalah penting. Algoritma yang mengubah isyarat domain masa ke komponen domain kekerapan dikenali sebagai transformasi Fourier diskret, atau DFT.

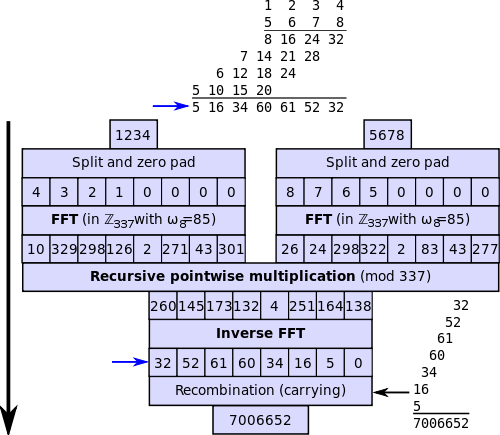
Fast Fourier Transform (FFT)

Transformasi Fourier Fast (FFT) adalah pelaksanaan DFT yang menghasilkan hasil yang hampir sama dengan DFT, tetapi ia sangat cekap dan lebih cepat yang sering mengurangkan masa pengiraan dengan ketara. Ia hanyalah algoritma pengiraan yang digunakan untuk pengiraan cepat dan cekap DFT. Pelbagai teknik pengiraan DFT cepat dikenali secara kolektif sebagai transformasi Fourier yang cepat, atau FFT. Gauss adalah yang pertama mencadangkan teknik untuk mengira pekali dalam trigonometri orbit asteroid pada tahun 1805. Walau bagaimanapun, tidak sampai tahun 1965 bahawa kertas seminal oleh Cooley dan Tukey menarik perhatian masyarakat sains dan kejuruteraan, yang juga meletakkan asas disiplin pemprosesan isyarat digital.

Perbezaan antara FFT dan DFT

1. Makna FFT dan DFT

Transformasi Fourier Diskret, atau hanya disebut sebagai DFT, adalah algoritma yang mengubah isyarat domain masa ke komponen domain frekuensi. DFT, seperti namanya, benar -benar diskret; Set data domain masa diskret diubah menjadi perwakilan frekuensi diskret. Secara ringkas, ia mewujudkan hubungan antara perwakilan domain masa dan perwakilan domain kekerapan. Transformasi Fourier Cepat, atau FFT, adalah algoritma pengiraan yang mengurangkan masa pengkomputeran dan kerumitan transformasi besar. FFT hanyalah algoritma yang digunakan untuk pengiraan pantas DFT.

2. Algoritma FFT dan DFT

Algoritma FFT yang paling biasa digunakan ialah algoritma Cooley-Tukey, yang dinamakan sempena J. W. Cooley dan John Tukey. Ini adalah algoritma membahagikan dan menakluki untuk pengiraan mesin siri Fourier yang kompleks. Ia memecahkan DFT ke DFT yang lebih kecil. Algoritma FFT lain termasuk algoritma Rader, algoritma transformasi Fourier Winograd, algoritma transformasi Z-CIRP, dan lain-lain, dll. Algoritma DFT boleh diprogramkan pada komputer digital tujuan umum atau dilaksanakan secara langsung oleh perkakasan khas. Algoritma FFT digunakan untuk mengira DFT urutan atau songsangnya. DFT boleh dilakukan sebagai O (n²) dalam kerumitan masa, sedangkan FFT mengurangkan kerumitan masa mengikut urutan O (nlogn).

3. Aplikasi FFT dan DFT

DFT boleh digunakan dalam banyak sistem pemprosesan digital merentasi pelbagai aplikasi seperti mengira spektrum frekuensi isyarat, menyelesaikan aplikasi pembezaan separa, pengesanan sasaran dari gema radar, analisis korelasi, pengkomputeran polinomial, analisis spektrum, dan banyak lagi. FFT telah digunakan secara meluas untuk pengukuran akustik di gereja dan dewan konsert. Aplikasi lain dari FFT termasuk analisis spektrum dalam pengukuran video analog, integer besar dan pendaraban polinomial, algoritma penapisan, pengkomputeran pengedaran isotop, mengira pekali siri Fourier, mengira convolutions, menghasilkan bunyi frekuensi rendah, merancang kinoforms, melakukan matrik berstruktur yang lebih padat, pemprosesan imej, dan pemprosesan, dan lebih.

FFT vs. DFT: carta perbandingan

Ringkasan FFT vs. Dft

Ringkas. Ia adalah algoritma yang mudah tetapi cukup memakan masa. Walau bagaimanapun, untuk mengurangkan masa pengkomputeran dan kerumitan transformasi besar, algoritma yang lebih kompleks tetapi kurang memakan masa seperti transformasi Fourier Fast boleh digunakan. FFT adalah pelaksanaan DFT yang digunakan untuk digunakan untuk pengiraan pantas DFT. Pendek kata, FFT dapat melakukan segala yang dilakukan oleh DFT, tetapi lebih efisien dan lebih cepat daripada DFT. Ini cara yang efisien untuk mengira DFT.