Perbezaan antara codomain dan julat

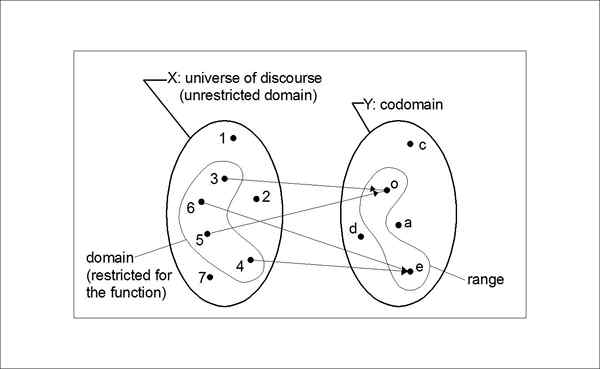
Kedua -dua codomain dan julat adalah tanggapan fungsi yang digunakan dalam matematik. Walaupun kedua -duanya berkaitan dengan output, perbezaan antara keduanya agak halus. Istilah "julat" kadang -kadang digunakan untuk merujuk kepada "Codomain".  Apabila anda membezakan antara keduanya, maka anda boleh merujuk kepada Codomain sebagai output fungsi diisytiharkan untuk menghasilkan. Walau bagaimanapun, jangkauan istilah adalah samar -samar kerana kadang -kadang boleh digunakan tepat seperti codomain digunakan. Mari ambil f: A -> b, di mana f Adakah fungsi dari A hingga B. Kemudian, B adalah codomain fungsi "f"Dan julat adalah set nilai yang berfungsi, yang dilambangkan oleh f (A). Julat boleh sama dengan atau kurang daripada codomain tetapi tidak boleh lebih besar daripada itu.

Sebagai contoh, biarkan a = 1, 2, 3, 4, 5 dan b = 1, 4, 8, 16, 25, 64, 125. Fungsinya f: A -> b ditakrifkan oleh f (x) = x ^3. Jadi disini,

Domain = tetapkan a

Codomain = set b, dan

Julat (r) = 1, 8, 64, 125

Julat harus menjadi kiub set A, tetapi kiub 3 (iaitu 27) tidak hadir dalam set B, jadi kita mempunyai 3 domain, tetapi kita tidak mempunyai 27 sama ada dalam codomain atau julat. Julatnya ialah subset codomain.

Apakah codomain fungsi?

"Codomain" fungsi atau hubungan adalah satu set nilai yang mungkin keluar daripadanya. Ini sebenarnya sebahagian daripada definisi fungsi, tetapi ia menyekat output fungsi. Contohnya, mari kita ambil notasi fungsi f: R -> r. Itu bermaksud itu f adalah fungsi dari nombor sebenar ke nombor sebenar. Di sini, Codomain adalah set nombor sebenar r atau set output yang mungkin keluar daripadanya. Domain juga merupakan set nombor sebenar r. Di sini, anda juga boleh menentukan fungsi atau hubungan untuk menyekat sebarang nilai negatif yang dihasilkan output. Secara ringkas, Codomain adalah satu set di mana nilai -nilai fungsi jatuh.

Biarkan n menjadi set nombor semulajadi dan hubungannya ditakrifkan sebagai r = (x, y): y = 2x, x, y ∈ N

Di sini, x dan y kedua -duanya selalu nombor semula jadi. Jadi,

Domain = n, dan

Codomain = n Itulah set nombor semula jadi.

Apakah pelbagai fungsi?

"Julat" fungsi disebut sebagai set nilai yang dihasilkan atau hanya sebagai set output nilai -nilainya. Julat istilah sering digunakan sebagai codomain, bagaimanapun, dalam erti kata yang lebih luas, istilah ini dikhaskan untuk subset codomain. Secara ringkas, julat adalah set semua nilai output fungsi dan fungsi adalah surat -menyurat antara domain dan julat. Dalam teori set asli, julat merujuk kepada imej fungsi atau codomain fungsi. Dalam matematik moden, julat sering digunakan untuk merujuk kepada imej fungsi. Buku -buku lama yang dirujuk kepada apa yang kini dikenali sebagai Codomain dan Buku Moden umumnya menggunakan julat istilah untuk merujuk kepada apa yang kini dikenali sebagai gambar. Sebilangan besar buku tidak menggunakan julat perkataan sama sekali untuk mengelakkan kekeliruan sama sekali.

Sebagai contoh, biarkan a = 1, 2, 3, 4 dan b = 1, 4, 9, 25, 64. Fungsinya f: A -> b ditakrifkan oleh f (x) = x ^2. Jadi di sini, tetapkan A adalah domain dan set B ialah codomain, dan julat = 1, 4, 9. Julat adalah kuadrat seperti yang ditakrifkan oleh fungsi, tetapi segi empat, iaitu 16, tidak hadir sama ada di codomain atau julatnya.

Perbezaan antara codomain dan julat

Definisi codomain dan julat

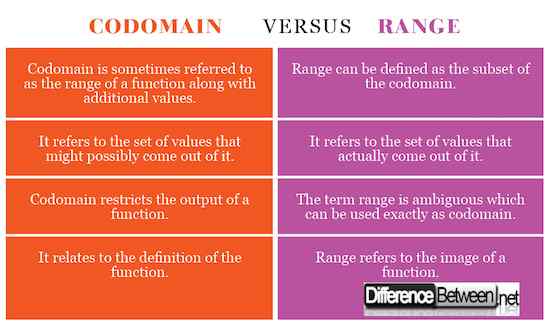
Kedua -dua terma itu berkaitan dengan output fungsi, tetapi perbezaannya adalah halus. Walaupun codomain fungsi adalah set nilai yang mungkin keluar daripadanya, ia sebenarnya sebahagian daripada definisi fungsi, tetapi ia menyekat output fungsi. Julat fungsi, sebaliknya, merujuk kepada set nilai yang sebenarnya dihasilkannya.

Tujuan codomain dan julat

Codomain fungsi adalah satu set nilai yang merangkumi julat tetapi mungkin termasuk beberapa nilai tambahan. Tujuan codomain adalah untuk menyekat output fungsi. Julatnya sukar untuk ditentukan kadang -kadang, tetapi set nilai yang lebih besar yang merangkumi keseluruhan julat boleh ditentukan. Codomain fungsi kadang -kadang berfungsi dengan tujuan yang sama seperti julat.

Contoh codomain dan julat

Jika A = 1, 2, 3, 4 dan B = 1, 2, 3, 4, 5, 6, 7, 8, 9 dan hubungannya f: A -> b ditakrifkan oleh f (x) = x ^2, kemudian codomain = set b = 1, 2, 3, 4, 5, 6, 7, 8, 9 dan julat = 1, 4, 9. Julatnya adalah kuadrat set A tetapi segi empat dari 4 (iaitu 16) tidak ada dalam set B (codomain) atau julatnya.

Codomain vs. Julat: Carta Perbandingan

Ringkasan Codomain vs. Julat

Walaupun kedua -duanya adalah istilah biasa yang digunakan dalam teori set asli, perbezaan antara keduanya agak halus. Codomain fungsi hanya boleh dirujuk sebagai set nilai output yang mungkin. Dalam istilah matematik, ia ditakrifkan sebagai output fungsi. Pelbagai fungsi, sebaliknya, boleh ditakrifkan sebagai set nilai yang sebenarnya keluar daripadanya. Walau bagaimanapun, istilah itu samar -samar, yang bermaksud ia boleh digunakan kadang -kadang tepat seperti codomain. Walau bagaimanapun, dalam matematik moden, julat digambarkan sebagai subset codomain, tetapi dalam erti kata yang lebih luas.