Perbezaan antara asymptote mendatar dan menegak

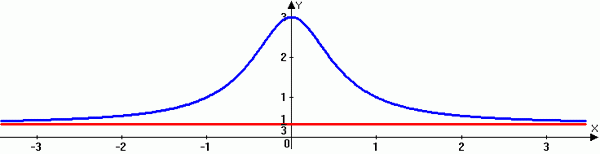
Sebelum kita masuk ke dalam topik asymptote mendatar dan menegak, mari kita cuba memahami apa sebenarnya asymptotes dan apakah peranan yang mereka mainkan dalam matematik. Dalam geometri projektif, asymptote adalah garis lurus yang mendekati lengkung yang diberikan sewenang -wenangnya tetapi tidak memenuhi jarak yang terbatas. Secara geometri, garis adalah asimtasi lengkung y = f (x), jika jarak antara garis dan titik 'p' pada lengkung mendekati sifar sebagai x dan y kedua -duanya cenderung ke tak terhingga. Grafik boleh mempunyai satu asymptote selari dengan setiap paksi. Sebenarnya, asymptote adalah sesuatu yang tidak ada secara fizikal - ia lebih seperti membuat kepercayaan.

Asymptote membantu menentukan tindakan atau bentuk sesuatu, tetapi ia bukan sebahagian daripada graf. Ini hanyalah garis khayalan yang membantu anda menggambarkan fungsi rasional. Apabila lengkung mendekati asymptote, ia semakin dekat dan lebih dekat dengan asymptote tetapi tidak pernah menyentuhnya. Oleh itu, asymptote membantu menentukan di mana graf fungsi boleh atau tidak boleh pergi. Bahawa dikatakan, terdapat tiga jenis asymptotes: asymptot menegak, mendatar dan serong. Tetapi kita hanya akan membincangkan asymptotes menegak dan asymptotes mendatar, dan melihat bagaimana untuk mengetahui yang sebenarnya sebenarnya.

Apa itu asymptote mendatar?

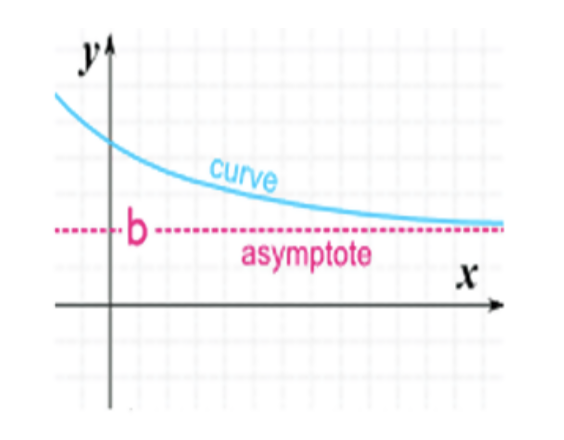
Asymptote mendatar adalah nilai malar pada graf yang menghampiri fungsi tetapi sebenarnya tidak mencapai. Ia menunjukkan apa yang sebenarnya berlaku pada lengkung kerana nilai x menjadi sangat besar atau sangat kecil. Dalam contoh grafik di atas, lengkung mendekati nilai malar b, tetapi tidak pernah mencapai, y = 0.

Garis y = b adalah asimtot mendatar graf 'f' jika f (x) -> b sebagai x -> ∞ atau x -> -∞

Untuk mencari asymptote mendatar fungsi rasional, tahap polinomial dalam pengangka dan penyebutnya dipertimbangkan.

• Sekiranya penyebut mempunyai kuasa pembolehubah tertinggi dalam persamaan fungsi, asymptote mendatar secara automatik paksi x atau y = 0.
• Jika kedua -dua pengangka dan penyebut mempunyai tahap yang sama, ambil pekali utama istilah tersebut dengan kuasa tertinggi dan membuat sebahagian kecil daripada mereka untuk mencari asimtot mendatar
• Jika pengangka mempunyai kuasa pembolehubah tertinggi dalam persamaan fungsi, fungsi tidak mempunyai asymptote mendatar; Grafik mungkin akan mempunyai asymptote serong.

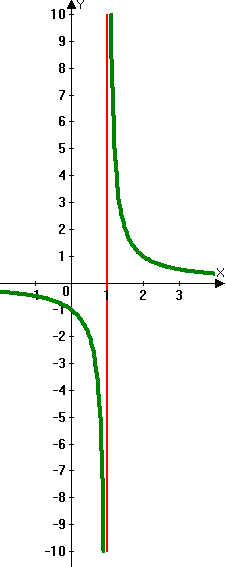
Apakah asymptote menegak?

Oleh kerana penyebut pecahan tidak boleh menjadi sifar, mempunyai pemboleh ubah di bahagian bawah jika pecahan boleh menjadi masalah. Sesetengah nilai domain 'x' menjadikan penyebut sifar dan fungsi akan melompat ke atas nilai ini dalam graf, mewujudkan asymptote menegak. Mereka adalah garis menegak yang ditarik dengan ringan atau dengan sengkang untuk menunjukkan bahawa mereka bukan sebahagian daripada graf.

Sekiranya nombor sebenar 'a' adalah sifar penyebut q (x), maka graf f (x) = p (x)/q (x), di mana p (x) dan q (x) tidak mempunyai umum faktor, mempunyai asymptote menegak, x = a.

Perbezaan antara asymptote mendatar dan menegak

Definisi

- Asymptote mendatar adalah nilai malar pada graf yang menghampiri fungsi tetapi sebenarnya tidak mencapai. Ia menunjukkan apa yang sebenarnya berlaku pada lengkung kerana nilai x menjadi sangat besar atau sangat kecil. Asymptotes menegak, sebaliknya, adalah garis menegak yang tidak kelihatan yang sesuai dengan sifar dalam penyebut pecahan rasional. Mereka adalah garis menegak yang ditarik dengan ringan atau dengan sengkang untuk menunjukkan bahawa mereka bukan sebahagian daripada graf.

Pengiraan

- Untuk menentukan asymptote mendatar fungsi rasional, tahap polinomial dalam pengangka dan penyebutnya dipertimbangkan. Sekiranya penyebut mempunyai kuasa pembolehubah tertinggi dalam persamaan fungsi, asymptote mendatar secara automatik paksi x atau y = 0. Jika kedua -dua pengangka dan penyebut mempunyai tahap yang sama, maka buat sebahagian kecil daripada pekali mereka untuk menentukan persamaan asymptote mendatar. Untuk menentukan asymptotes menegak fungsi rasional, tetapkan penyebut pecahan sama dengan sifar.

Contoh

- Mari kita cari asymptotes fungsi

Y = 3x²+9x-21 ∕ x²-25

Untuk mencari asymptot menegak, tetapkan penyebut pecahan sama dengan sifar.

x²-25 = 0

(x-5) (x+5) = 0

x = 5 dan x = - 5

Kedua -dua nombor ini adalah dua nilai yang tidak dapat dimasukkan ke dalam domain, jadi persamaan adalah asymptot menegak. Oleh itu, kedua -dua asymptot menegak adalah, x = 5 dan x = - 5.

Sekarang, untuk menentukan asymptote mendatar, lihat persamaan asal. Di sini, kuasa pemboleh ubah tertinggi adalah 2. Oleh kerana kedua -dua pengangka dan penyebut mempunyai tahap kuasa yang sama, membuat sebahagian kecil daripada pekali mereka:

y = 3x²/x²

y = 3/1

y = 3

Oleh itu, persamaan asymptote mendatar ialah, y = 3.

Asymptote mendatar vs. Asymptote Menegak: Carta Perbandingan

Ringkasan asymptote mendatar vs. Asymptote menegak

Asymptote membantu menentukan tindakan atau bentuk sesuatu, tetapi ia bukan sebahagian daripada graf. Asymptotes menegak menandakan tempat di mana fungsi tidak mempunyai domain. Anda menyelesaikan persamaan asymptot menegak dengan menetapkan penyebut pecahan sama dengan sifar. Asymptotes mendatar, sebaliknya, nyatakan apa yang berlaku pada lengkung sebagai nilai x menjadi sangat besar atau sangat kecil. Untuk mencari asymptote mendatar, anda perlu mempertimbangkan tahap polinomial dalam pengangka dan penyebut.