Perbezaan antara ujian parametrik dan nonparametrik

- 1887
- 84
- Mrs. Tomas Champlin
 Untuk membuat generalisasi mengenai populasi dari sampel, ujian statistik digunakan. Ujian statistik adalah teknik formal yang bergantung kepada taburan kebarangkalian, untuk mencapai kesimpulan mengenai kemunasabahan hipotesis. Ujian hipotesis ini yang berkaitan dengan perbezaan diklasifikasikan sebagai ujian parametrik dan nonparametrik.The Ujian Parametrik adalah salah satu yang mempunyai maklumat mengenai parameter penduduk.
Untuk membuat generalisasi mengenai populasi dari sampel, ujian statistik digunakan. Ujian statistik adalah teknik formal yang bergantung kepada taburan kebarangkalian, untuk mencapai kesimpulan mengenai kemunasabahan hipotesis. Ujian hipotesis ini yang berkaitan dengan perbezaan diklasifikasikan sebagai ujian parametrik dan nonparametrik.The Ujian Parametrik adalah salah satu yang mempunyai maklumat mengenai parameter penduduk.
Sebaliknya, Ujian nonparametrik adalah salah satu di mana penyelidik tidak tahu mengenai parameter penduduk. Oleh itu, baca sepenuhnya artikel ini, untuk mengetahui perbezaan yang signifikan antara ujian parametrik dan nonparametrik.
Kandungan: Ujian Parametrik vs Ujian Nonparametrik
- Carta Perbandingan
- Definisi
- Perbezaan utama
- Hipotesis ujian hierarki
- Ujian bersamaan
- Kesimpulan
Carta Perbandingan
| Asas untuk perbandingan | Ujian Parametrik | Ujian nonparametrik |
|---|---|---|
| Makna | Ujian statistik, di mana andaian spesifik dibuat mengenai parameter populasi dikenali sebagai ujian parametrik. | Ujian statistik yang digunakan dalam kes pembolehubah bebas bukan metrik, dipanggil ujian bukan parametrik. |
| Asas statistik ujian | Pengedaran | Sewenang -wenangnya |
| Tahap pengukuran | Selang atau nisbah | Nominal atau ordinal |
| Ukuran kecenderungan pusat | Maksudnya | Median |
| Maklumat mengenai penduduk | Dikenali sepenuhnya | Tidak ada |
| Kebolehgunaan | Pembolehubah | Pembolehubah dan atribut |
| Ujian korelasi | Pearson | Spearman |
Definisi ujian parametrik
Ujian parametrik adalah ujian hipotesis yang memberikan generalisasi untuk membuat kenyataan mengenai min penduduk induk. Ujian t berdasarkan statistik t pelajar, yang sering digunakan dalam hal ini.
Statistik T terletak pada andaian asas bahawa terdapat pengagihan normal pemboleh ubah dan min yang diketahui atau dianggap dikenali. Varians penduduk dikira untuk sampel. Diandaikan bahawa pembolehubah yang menarik, dalam populasi diukur pada skala selang waktu.
Definisi ujian nonparametrik
Ujian nonparametrik ditakrifkan sebagai ujian hipotesis yang tidak berdasarkan kepada andaian yang mendasari, i.e. ia tidak memerlukan pengedaran penduduk dilambangkan oleh parameter tertentu.
Ujian ini terutamanya berdasarkan perbezaan medan. Oleh itu, ia secara bergantian dikenali sebagai ujian bebas pengedaran. Ujian mengandaikan bahawa pembolehubah diukur pada tahap nominal atau ordinal. Ia digunakan apabila pembolehubah bebas tidak metrik.
Perbezaan utama antara ujian parametrik dan nonparametrik
Perbezaan asas antara ujian parametrik dan nonparametrik dibincangkan dalam perkara berikut:
- Ujian statistik, di mana andaian spesifik dibuat mengenai parameter populasi dikenali sebagai ujian parametrik. Ujian statistik yang digunakan dalam kes pembolehubah bebas bukan metrik dipanggil ujian nonparametrik.
- Dalam ujian parametrik, statistik ujian adalah berdasarkan pengedaran. Sebaliknya, statistik ujian sewenang -wenangnya dalam kes ujian nonparametrik.
- Dalam ujian parametrik, diandaikan bahawa pengukuran pemboleh ubah kepentingan dilakukan pada tahap selang atau nisbah. Berbanding dengan ujian nonparametrik, di mana pemboleh ubah kepentingan diukur pada skala nominal atau ordinal.
- Secara umum, ukuran kecenderungan pusat dalam ujian parametrik adalah bermakna, manakala dalam kes ujian nonparametrik adalah median.
- Dalam ujian parametrik, terdapat maklumat lengkap mengenai penduduk. Sebaliknya, dalam ujian nonparametrik, tidak ada maklumat mengenai penduduk.
- Kebolehgunaan ujian parametrik adalah untuk pembolehubah sahaja, sedangkan ujian nonparametrik terpakai kepada kedua -dua pembolehubah dan atribut.
- Untuk mengukur tahap hubungan antara dua pembolehubah kuantitatif, koefisien korelasi Pearson digunakan dalam ujian parametrik, manakala korelasi pangkat Spearman digunakan dalam ujian nonparametrik.
Hipotesis ujian hierarki
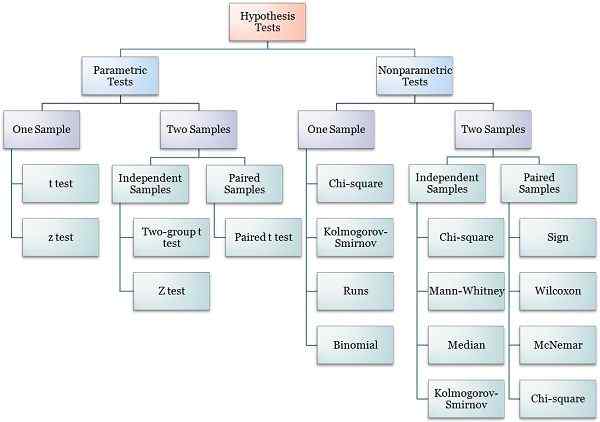
Ujian bersamaan
| Ujian Parametrik | Ujian bukan parametrik |
|---|---|
| Ujian sampel bebas t | Ujian Mann-Whitney |
| Ujian sampel yang dipasangkan t | Wilcoxon menandatangani ujian pangkat |
| Satu cara analisis varians (ANOVA) | Ujian Kruskal Wallis |
| Satu cara mengulangi langkah analisis varians | Anova Friedman |
Kesimpulan
Untuk membuat pilihan antara parametrik dan ujian nonparametrik tidak mudah bagi penyelidik yang menjalankan analisis statistik. Untuk melaksanakan hipotesis, jika maklumat tentang populasi diketahui sepenuhnya, dengan cara parameter, maka ujian itu dikatakan sebagai ujian parametrik sedangkan, jika tidak ada pengetahuan tentang penduduk dan diperlukan untuk menguji hipotesis terhadap penduduk, maka maka Ujian yang dijalankan dianggap sebagai ujian nonparametrik.

