Perbezaan antara ujian t dan ujian f
- 1329
- 361
- Brandon Haag
Ujian hipotesis bermula dengan menubuhkan premis, yang diikuti dengan memilih tahap kepentingan. Seterusnya, kita mesti memilih statistik ujian, i.e. ujian t atau ujian f. Manakala ujian t digunakan untuk membandingkan dua sampel yang berkaitan, f-test digunakan untuk menguji kesamaan dua populasi.
Hipotesis adalah cadangan mudah yang dapat dibuktikan atau dibuktikan melalui pelbagai teknik saintifik dan mewujudkan hubungan antara pembolehubah bebas dan beberapa bergantung. Ia mampu diuji dan disahkan untuk menentukan kesahihannya, dengan peperiksaan yang tidak berat sebelah. Ujian hipotesis percubaan untuk menjelaskan, sama ada atau tidak anggapan itu sah atau tidak.
Bagi penyelidik, adalah penting untuk memilih ujian yang tepat untuk hipotesisnya kerana keseluruhan keputusan mengesahkan atau menolak hipotesis nol itu berdasarkannya. Ambil bacaan artikel yang diberikan untuk memahami perbezaan antara ujian t dan ujian F.
Kandungan: t-test vs f-test
- Carta Perbandingan
- Definisi
- Perbezaan utama
- Kesimpulan
Carta Perbandingan
| Asas untuk perbandingan | Ujian t | F-test |
|---|---|---|
| Makna | Ujian t adalah ujian hipotesis univariat, yang digunakan apabila sisihan piawai tidak diketahui dan saiz sampel kecil. | Ujian F adalah ujian statistik, yang menentukan kesamaan variasi kedua-dua populasi biasa. |
| Statistik ujian | T-Statistik Mengikuti Pelajar T-Distribusi, Di bawah Hipotesis Nol. | F-Statistik Mengikuti Snedecor F-Distribusi, Di bawah Hipotesis Nol. |
| Permohonan | Membandingkan cara dua populasi. | Membandingkan dua variasi penduduk. |
Definisi ujian t
Ujian t adalah satu bentuk ujian hipotesis statistik, berdasarkan pengedaran t-statistik dan t pelajar untuk mengetahui nilai p (kebarangkalian) yang boleh digunakan untuk menerima atau menolak hipotesis nol.
Analisis ujian t Jika cara dua set data sangat berbeza antara satu sama lain, i.e. Sama ada maksud penduduk adalah sama atau berbeza dari min standard. Ia juga boleh digunakan untuk menentukan sama ada garis regresi mempunyai cerun yang berbeza dari sifar. Ujian ini bergantung pada beberapa andaian, iaitu:
- Penduduknya tidak terbatas dan normal.
- Varians penduduk tidak diketahui dan dianggarkan dari sampel.
- Maksudnya dikenali.
- Pemerhatian sampel adalah rawak dan bebas.
- Saiz sampel kecil.
- H0 mungkin satu sisi atau dua sisi.
Purata dan sisihan piawai kedua -dua sampel digunakan untuk membuat perbandingan di antara mereka, seperti itu:
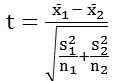di mana,
x̄1 = Bermaksud dataset pertama
x̄2 = Maksud dataset kedua
S1 = Sisihan piawai dataset pertama
S2 = Sisihan piawai dataset kedua
n1 = Saiz dataset pertama
n2 = Saiz dataset kedua
Definisi F-Test
Ujian F digambarkan sebagai jenis ujian hipotesis, yang berdasarkan snedecor f-distribusi, di bawah hipotesis nol. Ujian dilakukan apabila tidak diketahui sama ada kedua -dua populasi mempunyai varians yang sama.
Ujian F juga boleh digunakan untuk memeriksa sama ada data mematuhi model regresi, yang diperoleh melalui analisis persegi paling sedikit. Apabila terdapat pelbagai analisis regresi linear, ia mengkaji kesahihan keseluruhan model atau menentukan sama ada mana -mana pembolehubah bebas mempunyai hubungan linear dengan pemboleh ubah bergantung. Sejumlah ramalan dapat dibuat, perbandingan dua dataset tersebut. Ekspresi nilai F-Test adalah dalam nisbah variasi dua pemerhatian, yang ditunjukkan seperti di bawah:
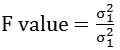Di mana, σ2 = varians
Andaian yang bergantung kepada F-Test adalah:
- Penduduk diedarkan secara normal.
- Sampel telah ditarik secara rawak.
- Pemerhatian adalah bebas.
- H0 mungkin satu sisi atau dua sisi.
Perbezaan utama antara ujian t dan ujian f
Perbezaan antara ujian t dan ujian F boleh ditarik dengan jelas berdasarkan alasan berikut:
- Ujian hipotesis univariat yang digunakan apabila sisihan piawai tidak diketahui dan saiz sampel kecil adalah ujian t. Sebaliknya, ujian statistik, yang menentukan kesamaan variasi dua dataset biasa, dikenali sebagai F-Test.
- Ujian t didasarkan pada t-statistik mengikuti pengagihan t pelajar, di bawah hipotesis nol. Sebaliknya, asas ujian F adalah f-statistik mengikuti snedecor f-distribusi, di bawah hipotesis nol.
- Ujian t digunakan untuk membandingkan cara dua populasi. Sebaliknya, ujian F digunakan untuk membandingkan dua variasi penduduk.
Kesimpulan
Ujian t dan ujian F adalah dua, bilangan jenis ujian statistik yang digunakan untuk ujian hipotesis dan memutuskan sama ada kita akan menerima hipotesis nol atau menolaknya. Ujian hipotesis tidak mengambil keputusan itu sendiri, sebaliknya ia membantu penyelidik dalam membuat keputusan.