Perbezaan antara permutasi dan gabungan

- 2703
- 606
- Mrs. Ted Marks
 Dalam matematik, anda mungkin pernah mendengar tanggapan mengenai permutasi dan kombinasi akhir kali, tetapi adakah anda pernah membayangkan bahawa kedua -dua ini adalah konsep yang berbeza? Perbezaan asas antara permutasi dan gabungan adalah urutan objek, dalam permutasi Perintah objek sangat penting, i.e. Pengaturan mestilah dalam urutan yang ditetapkan bilangan objek, hanya diambil beberapa atau semua pada satu masa.
Dalam matematik, anda mungkin pernah mendengar tanggapan mengenai permutasi dan kombinasi akhir kali, tetapi adakah anda pernah membayangkan bahawa kedua -dua ini adalah konsep yang berbeza? Perbezaan asas antara permutasi dan gabungan adalah urutan objek, dalam permutasi Perintah objek sangat penting, i.e. Pengaturan mestilah dalam urutan yang ditetapkan bilangan objek, hanya diambil beberapa atau semua pada satu masa.
Bertentangan dengan ini, dalam hal a gabungan, Pesanan tidak penting sama sekali. Bukan sahaja dalam matematik tetapi juga dalam kehidupan praktikal, kita melalui dua konsep ini secara berkala. Walaupun, kita tidak pernah menyedarinya. Oleh itu, bacalah artikel dengan teliti, untuk mengetahui bagaimana kedua -dua konsep ini berbeza.
Kandungan: Permutasi vs gabungan
- Carta Perbandingan
- Definisi
- Perbezaan utama
- Contoh
- Kesimpulan
Carta Perbandingan
| Asas untuk perbandingan | Permutasi | Gabungan |
|---|---|---|
| Makna | Permutasi merujuk kepada cara yang berbeza untuk mengatur satu set objek dalam urutan berurutan. | Gabungan merujuk kepada beberapa cara memilih barang dari satu set objek yang besar, sehingga pesanan mereka tidak penting. |
| Pesanan | Relevan | Tidak relevan |
| Menandakan | Pengaturan | Pemilihan |
| Apa itu? | Elemen yang diperintahkan | Set tidak teratur |
| Jawapan | Berapa banyak susunan yang berbeza dapat dibuat dari satu set objek yang diberikan? | Berapa banyak kumpulan yang berbeza boleh dipilih dari kumpulan objek yang lebih besar? |
| Terbitan | Pelbagai permutasi dari satu gabungan. | Gabungan tunggal dari satu permutasi. |
Definisi permutasi
Kami mentakrifkan permutasi sebagai cara yang berbeza untuk mengatur beberapa atau semua ahli set dalam urutan tertentu. Ia membayangkan semua susunan atau penyusunan semula yang mungkin berlaku, ke dalam urutan yang boleh dibezakan.
Sebagai contoh, Semua permutasi yang mungkin dibuat dengan huruf x, y, z -
- Dengan mengambil ketiga -tiga mereka adalah XYZ, XZY, YXZ, YZX, ZXY, ZYX.
- Dengan mengambil dua pada satu masa ialah XY, XZ, YX, YZ, ZX, ZY.
Jumlah bilangan permutasi yang mungkin bagi perkara N, yang diambil pada satu masa, boleh dikira sebagai:
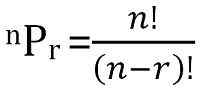
Definisi gabungan
Gabungan ini ditakrifkan sebagai cara yang berbeza, memilih kumpulan, dengan mengambil beberapa atau semua ahli set, tanpa perintah berikut.
Sebagai contoh, Semua kombinasi yang mungkin dipilih dengan huruf m, n, o -
- Apabila tiga daripada tiga huruf dipilih, maka satu -satunya kombinasi adalah MNO
- Apabila dua daripada tiga huruf dipilih, maka kemungkinan kombinasi adalah Mn, tidak, om.
Jumlah bilangan kombinasi yang mungkin bagi perkara N, yang diambil pada satu masa boleh dikira sebagai:
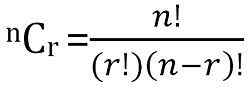
Perbezaan utama antara permutasi dan gabungan
Perbezaan antara permutasi dan gabungan ditarik dengan jelas berdasarkan alasan berikut:
- Istilah permutasi merujuk kepada beberapa cara mengatur satu set objek dalam urutan berurutan. Gabungan membayangkan beberapa cara memilih barang dari sekumpulan objek yang besar, sehingga pesanan mereka tidak relevan.
- Titik membezakan utama antara kedua -dua konsep matematik ini adalah perintah, penempatan, dan kedudukan, i.e. dalam ciri -ciri permutasi yang disebutkan di atas tidak penting, yang tidak penting dalam hal gabungan.
- Permutasi menandakan beberapa cara untuk mengatur perkara, orang, digit, abjad, warna, dll. Sebaliknya, gabungan menunjukkan cara yang berbeza untuk memilih item menu, makanan, pakaian, subjek, dan lain -lain.
- Permutasi tidak lain hanyalah kombinasi yang diperintahkan manakala gabungan menyiratkan set yang tidak teratur atau berpasangan nilai dalam kriteria tertentu.
- Banyak permutasi dapat diperoleh dari satu gabungan. Sebaliknya, hanya satu kombinasi yang dapat diperoleh dari satu permutasi.
- Permutasi Jawapan Berapa banyak pengaturan yang berbeza dapat dibuat dari satu set objek tertentu? Berbanding dengan gabungan yang menerangkan berapa banyak kumpulan yang berbeza dapat dipilih dari sekumpulan objek yang lebih besar?
Contoh
Katakan, terdapat situasi di mana anda perlu mengetahui jumlah sampel yang mungkin dua daripada tiga objek A, B, C. Dalam soalan ini, pertama sekali, anda perlu memahami, sama ada soalan itu berkaitan dengan permutasi atau gabungan dan satu -satunya cara untuk mencari ini adalah untuk memeriksa sama ada perintah itu penting atau tidak.
Sekiranya pesanan itu penting, maka persoalannya berkaitan dengan permutasi, dan sampel yang mungkin akan, AB, BA, BC, CB, AC, CA. Di mana, AB berbeza dari BA, BC berbeza dari CB dan AC adalah CA yang berbeza.
Sekiranya pesanan itu tidak relevan, maka persoalannya berkaitan dengan gabungan, dan sampel yang mungkin akan menjadi AB, BC dan CA.
Kesimpulan
Dengan perbincangan di atas, jelas bahawa permutasi dan gabungan adalah istilah yang berbeza, yang digunakan dalam matematik, statistik, penyelidikan dan kehidupan seharian kita. Titik yang perlu diingat, mengenai kedua -dua konsep ini ialah, untuk satu set objek yang diberikan, permutasi akan sentiasa lebih tinggi daripada gabungannya.
- « Perbezaan antara perakaunan dan pengauditan
- Perbezaan antara usahasama dan persekutuan strategik »

