Perbezaan antara sisihan piawai dan ralat standard

- 4544
- 1074
- David Collier
 Sisihan piawai ditakrifkan sebagai ukuran mutlak penyebaran siri. Ia menjelaskan jumlah standard variasi di kedua -dua belah min. Ia sering disalah anggap kesilapan standard, kerana ia berdasarkan sisihan piawai dan saiz sampel.
Sisihan piawai ditakrifkan sebagai ukuran mutlak penyebaran siri. Ia menjelaskan jumlah standard variasi di kedua -dua belah min. Ia sering disalah anggap kesilapan standard, kerana ia berdasarkan sisihan piawai dan saiz sampel.
Kesalahan biasa digunakan untuk mengukur ketepatan statistik anggaran. Ia digunakan terutamanya dalam proses ujian hipotesis dan menganggarkan selang.
Ini adalah dua konsep statistik penting, yang digunakan secara meluas dalam bidang penyelidikan. Perbezaan antara sisihan piawai dan ralat standard adalah berdasarkan perbezaan antara penerangan data dan kesimpulannya.
Kandungan: sisihan piawai vs ralat standard
- Carta Perbandingan
- Definisi
- Perbezaan utama
- Kesimpulan
Carta Perbandingan
| Asas untuk perbandingan | Sisihan piawai | Kesalahan biasa |
|---|---|---|
| Makna | Sisihan piawai membayangkan ukuran penyebaran set nilai dari maksudnya. | Ralat standard menceritakan ukuran ketepatan statistik anggaran. |
| Statistik | Penjelasan | Kesimpulan |
| Langkah -langkah | Berapa banyak pemerhatian berbeza antara satu sama lain. | Betapa tepatnya sampel itu bermakna kepada penduduk yang benar. |
| Pengedaran | Pengagihan pemerhatian mengenai lengkung biasa. | Pengagihan anggaran mengenai lengkung biasa. |
| Formula | Akar varians persegi | Sisihan piawai dibahagikan dengan akar kuadrat saiz sampel. |
| Meningkatkan saiz sampel | Memberikan ukuran sisihan piawai yang lebih spesifik. | Mengurangkan ralat standard. |
Definisi sisihan piawai
Sisihan piawai, adalah ukuran penyebaran siri atau jarak dari standard. Pada tahun 1893, Karl Pearson mencipta tanggapan sisihan piawai, yang tidak diragukan lagi ukuran yang paling banyak digunakan, dalam kajian penyelidikan.
Ia adalah akar kuadrat dari purata kuadrat penyimpangan dari maksudnya. Dalam erti kata lain, untuk set data yang diberikan, sisihan piawai adalah penyesuaian akar-rata-persegi, dari aritmetik min. Bagi seluruh penduduk, ia ditunjukkan oleh huruf Yunani 'sigma (σ)', dan untuk sampel, ia diwakili oleh huruf Latin 's'.
Sisihan piawai adalah ukuran yang mengukur tahap penyebaran set pemerhatian. Semakin jauh titik data dari nilai min, semakin besar sisihan dalam set data, yang mewakili titik data bertaburan ke atas nilai yang lebih luas dan sebaliknya.
- Untuk data yang tidak dikelaskan:
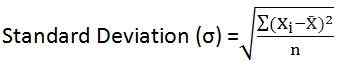
- Untuk pengagihan frekuensi dikumpulkan:

Definisi ralat standard
Anda mungkin mendapati bahawa sampel yang berbeza, dengan saiz yang sama, yang diambil dari populasi yang sama, akan memberikan nilai statistik yang pelbagai di bawah pertimbangan, i.e. Maksud sampel. Ralat Standard (SE) menyediakan, sisihan piawai dalam nilai yang berbeza dari min sampel. Ia digunakan untuk membuat perbandingan antara cara sampel di seluruh populasi.
Singkatnya, kesilapan standard statistik hanyalah sisihan piawai pengedaran pensampelannya. Ia mempunyai peranan yang besar untuk memainkan ujian hipotesis statistik dan anggaran selang. Ia memberikan idea tentang ketepatan dan kebolehpercayaan anggaran. Semakin kecil kesilapan standard, semakin besar adalah keseragaman pengedaran teoritis dan sebaliknya.
- Formula: Ralat standard untuk min sampel = σ/√n
Di mana, σ adalah sisihan piawai penduduk
Perbezaan utama antara sisihan piawai dan ralat standard
Titik yang dinyatakan di bawah adalah besar setakat ini perbezaan antara sisihan piawai berkenaan:
- Sisihan piawai adalah ukuran yang menilai jumlah variasi dalam set pemerhatian. Mengukur kesilapan standard ketepatan anggaran, i.e. ia adalah ukuran kebolehubahan pengagihan teori statistik.
- Sisihan piawai adalah statistik deskriptif, sedangkan ralat standard adalah statistik inferensial.
- Sisihan piawai mengukur sejauh mana nilai individu dari nilai min. Sebaliknya, sejauh mana maksud sampel adalah maksud penduduk.
- Sisihan piawai adalah pengagihan pemerhatian dengan merujuk kepada lengkung biasa. Sebaliknya, ralat standard adalah pengagihan anggaran dengan merujuk kepada lengkung normal.
- Sisihan piawai ditakrifkan sebagai akar kuadrat dari varians. Sebaliknya, ralat standard digambarkan sebagai sisihan piawai yang dibahagikan dengan akar kuadrat saiz sampel.
- Apabila saiz sampel dibangkitkan, ia memberikan ukuran sisihan piawai yang lebih khusus. Tidak seperti, ralat standard apabila saiz sampel meningkat, ralat standard cenderung menurun.
Kesimpulan
Secara keseluruhannya, sisihan piawai dianggap sebagai salah satu ukuran terbaik penyebaran, yang mengukur penyebaran nilai dari nilai pusat. Sebaliknya, ralat standard digunakan terutamanya untuk memeriksa kebolehpercayaan dan ketepatan anggaran dan sebagainya, semakin kecil kesilapan, semakin besar kebolehpercayaan dan ketepatannya.

