Perbezaan antara kesatuan dan persimpangan

Sebelum memahami perbezaan antara dua kesatuan pengendali dan persimpangan, mari kita fahami konsep teori set terlebih dahulu. Teori Tetapkan adalah cabang asas matematik yang ditetapkan kajian, terutamanya sama ada objek milik, atau tidak tergolong dalam, satu set objek yang entah bagaimana matematik yang relevan. Set pada dasarnya adalah koleksi objek yang jelas, yang mungkin atau mungkin tidak relevan matematik, seperti nombor atau fungsi. Objek dalam satu set dipanggil elemen, yang boleh menjadi seperti nombor, orang, kereta, negeri, dll. Hampir apa sahaja dan sebilangan elemen dapat dikumpulkan bersama untuk membuat satu set.

Secara ringkas, set adalah koleksi bilangan unsur yang tidak teratur yang boleh dianggap sebagai objek tunggal secara keseluruhan. Mari kita fahami konsep asas dan notasi satu set dan bagaimana ia diwakili. Semuanya bermula dengan hubungan binari antara objek x dan set a. Untuk mewakili jika x adalah ahli set A, notasi x ∊ a digunakan, sementara x ∉ a menunjukkan bahawa objek x tidak tergolong dalam set a. Ahli satu set disenaraikan dalam pendakap keriting. Sebagai contoh, set nombor perdana kurang daripada 10 boleh ditulis sebagai 2, 3, 5, 7. Begitu juga, satu set nombor kurang daripada 10 boleh ditulis sebagai 2, 4, 6, 8. Hypothetically, hampir mana -mana set terhingga boleh diwakili oleh ahli -ahlinya.

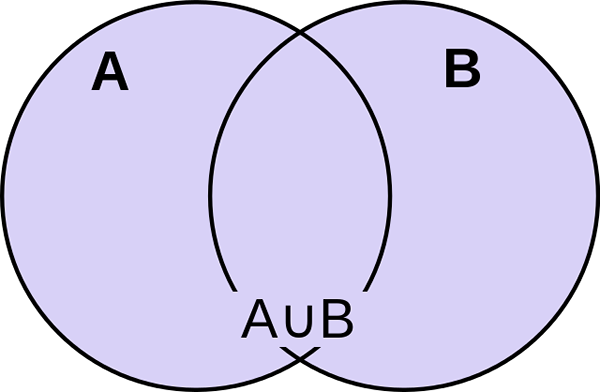
Apa itu kesatuan set?

Kesatuan dua set A dan B ditakrifkan sebagai set elemen yang tergolong dalam sama ada A atau B, atau mungkin kedua -duanya. Ia hanya ditakrifkan sebagai set semua elemen atau ahli yang berbeza, di mana ahli -ahli milik mana -mana set ini. Pengendali kesatuan sepadan dengan logik atau dan diwakili oleh simbol ∪. Ia adalah set terkecil yang mengandungi semua elemen kedua -dua set. Sebagai contoh, jika ditetapkan ialah 1, 2, 3, 4, 5 dan set B ialah 3, 4, 6, 7, 9, maka Kesatuan A dan B diwakili oleh A∪B dan ditulis sebagai 1, 2, 3, 4, 5, 6, 7, 9. Oleh kerana nombor 3 dan 4 hadir di kedua -dua set A dan B, tidak perlu menyenaraikannya dua kali. Jelas bahawa bilangan unsur kesatuan a dan b lebih kecil daripada jumlah set individu, kerana beberapa nombor adalah biasa di kedua -dua set.

A = 1, 3, 5, 7, 9

B = 3, 6, 9, 12, 15

A∪b = 1, 3, 5, 6, 7, 9, 12, 15

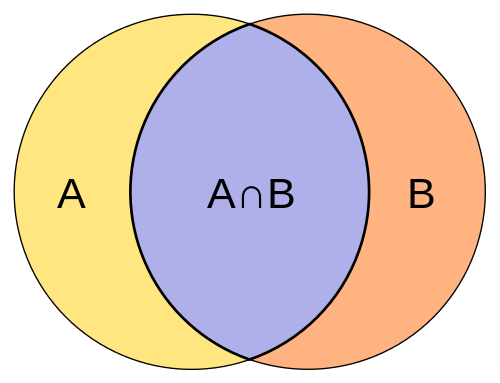
Apakah persimpangan set?

Persimpangan dua set A dan B ditakrifkan sebagai set elemen yang dimiliki oleh A dan B. Ia hanya ditakrifkan sebagai set yang mengandungi semua elemen set A yang juga tergolong dalam set B, dan juga semua elemen set b milik set a. Pengendali persimpangan sepadan dengan logik dan dan diwakili oleh simbol ∩. Sebaliknya, persimpangan dua set adalah set terbesar yang mengandungi semua elemen yang biasa bagi kedua -dua set. Sebagai contoh, jika ditetapkan ialah 1, 2, 3, 4, 5 dan set B ialah 3, 4, 6, 7, 9, maka persimpangan A dan B diwakili oleh A∩B dan ditulis sebagai 3, 4. Hanya nombor 3 dan 4 yang biasa di kedua -dua set A dan B, mereka dipanggil persimpangan set.

A = 2, 3, 5, 7, 11

B = 1, 3, 5, 7, 9, 11

A∩b = 3, 5, 7, 11

Perbezaan antara kesatuan dan persimpangan set

1. Asas - Kesatuan dua set A dan B ditakrifkan sebagai set elemen yang dimiliki sama ada A atau B, atau mungkin kedua -duanya, sedangkan persimpangan dua set ditakrifkan sebagai set elemen yang dimiliki oleh A dan B.
2. Perwakilan simbolik - Kesatuan dua set diwakili oleh simbol "∪", sedangkan persimpangan dua set diwakili oleh simbol "∩".
3. Relevan logik - Kesatuan dua set sepadan dengan "atau" logik manakala persimpangan dua set sesuai dengan "dan".
4. Contoh - Biarkan a = a, e, i, o, u dan

B = A, B, C, D, E, F

A∪b = a, b, c, d, e, f, i, o, u

A∩b = a, e

Kesatuan vs. Persimpangan: carta perbandingan

Ringkasan Kesatuan vs. Persimpangan

Kedua -dua kesatuan dan persimpangan adalah dua operasi asas di mana set boleh digabungkan dan berkaitan antara satu sama lain. Dari segi teori yang ditetapkan, kesatuan adalah set semua unsur yang ada dalam set, atau dalam kedua -dua, sedangkan persimpangan adalah set semua unsur yang berbeza yang dimiliki oleh kedua -dua set. Kesatuan dua set A dan B dilambangkan sebagai "A∪b", sedangkan persimpangan A dan B dilambangkan sebagai "A∩b". Set hanyalah koleksi objek yang jelas, seperti nombor dan fungsi, dan objek dalam set dipanggil sebagai elemen.