Perbezaan antara korelasi dan regresi

Kedua -dua korelasi dan regresi adalah alat statistik yang menangani dua atau lebih pembolehubah. Walaupun kedua -duanya berkaitan dengan perkara yang sama, terdapat perbezaan antara kedua -dua. Perbezaan, antara keduanya dijelaskan di bawah.

Makna

Korelasi istilah dengan merujuk kepada dua atau lebih pembolehubah menandakan bahawa pembolehubah berkaitan dengan beberapa cara. Analisis korelasi menentukan sama ada hubungan antara dua pembolehubah wujud, dan kekuatan hubungan. Jika dua pembolehubah x (bebas) dan y (bergantung) sangat berkaitan bahawa variasi dalam magnitud pembolehubah bebas disertai, dengan variasi magnitud pemboleh ubah bergantung maka kedua -dua pembolehubah dikatakan berkorelasi.

Korelasi boleh linear atau tidak linear. Korelasi linear adalah satu di mana pembolehubah sangat berkaitan sehingga perubahan nilai satu pembolehubah akan menyebabkan perubahan nilai pembolehubah lain secara konsisten. In a linear correlation the scattered points related to the respective values ​​of dependent and independent variables would cluster around a non-horizontal straight line, although a horizontal straight line would also indicate a linear relationship between the variables if a straight line could connect the points representing pembolehubah.

Analisis regresi, sebaliknya, menggunakan data yang ada untuk menentukan hubungan matematik antara pembolehubah yang boleh digunakan untuk menentukan nilai pemboleh ubah bergantung berkenaan dengan sebarang nilai pembolehubah bebas.

Orientasi statistik

Korelasi berkenaan dengan pengukuran kekuatan persatuan atau intensiti hubungan, di mana regresi berkenaan dengan ramalan nilai pemboleh ubah bergantung berkaitan dengan nilai yang diketahui pemboleh ubah bebas. Ini dapat dijelaskan dengan formula berikut.

Koefisien korelasi atau korelasi pekali (R) antara X & Y dijumpai dengan formula berikut;

r = kovarians (x, y)/σx.σy, cov (x, y) = σxy/n - (σx/n) (σy/n), σx & σy adalah sisihan piawai x dan y masing -masing, dan, -1 < r 0, then correlation coefficient between x and y = correlation coefficient between u and v.

Koefisien korelasi r adalah nombor tulen dan bebas daripada unit pengukuran. Oleh itu jika x adalah ketinggian (inci) dan y adalah berat (lbs.) orang di rantau tertentu, maka r tidak dalam inci atau di lbs., Tetapi hanya nombor.

Persamaan regresi dijumpai dengan formula berikut;

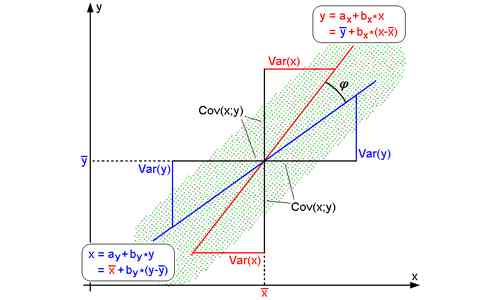
Persamaan regresi y pada x (untuk mengetahui anggaran y) adalah y - y '= byx (x -x‾), byx dipanggil pekali regresi y pada x. Persamaan regresi x pada y (untuk mengetahui anggaran x) ialah x - x '= bxy (y -y‾), bxy dipanggil pekali regresi x pada y.

Analisis korelasi tidak menganggap kebergantungan mana -mana pemboleh ubah pada pemboleh ubah lain, tidak juga cuba untuk mengetahui hubungan antara kedua -dua. Ia hanya menganggarkan tahap hubungan antara pembolehubah. Dalam erti kata lain, analisis korelasi menguji saling ketergantungan pembolehubah. Analisis regresi di sisi lain menerangkan pergantungan pembolehubah pembolehubah atau tindak balas bergantung pada pemboleh ubah bebas atau penjelasan/s. Analisis regresi mengandaikan bahawa terdapat hubungan kausal sehala antara pemboleh ubah penjelasan dan tindak balas, dan tidak mengambil kira sama ada hubungan kausal adalah positif atau negatif. Untuk korelasi kedua -dua nilai pembolehubah bergantung dan bebas adalah rawak, tetapi untuk nilai regresi pembolehubah bebas tidak perlu rawak.

Ringkasan

1. Analisis korelasi adalah ujian antara ketergantungan antara dua pembolehubah. Analisis regresi memberikan formula matematik untuk menentukan nilai pemboleh ubah bergantung berkenaan dengan nilai pembolehubah bebas/s.

2. Koefisien korelasi adalah bebas daripada pilihan asal dan skala, tetapi pekali regresi tidak begitu.

Untuk korelasi nilai -nilai kedua -dua pembolehubah harus rawak, tetapi ini tidak begitu untuk pekali regresi.

Bibliografi

1. Das, n. G., (1998), Kaedah Statistik, Calcutta

2. Korelasi & Regresi, boleh didapati di www.le.ac.UK/BL/GAT/Virtualfc/Stats/Regresi

3. Regresi & Korelasi, boleh didapati di www.Abyss.Uoregon.edu