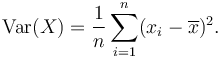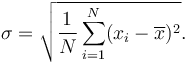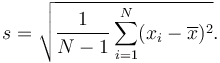Sisihan piawai vs. Varians
- 952
- 43
- Mrs. Ted Marks
Sisihan piawai dan varians Adakah ukuran statistik penyebaran data, i.e., Mereka mewakili berapa banyak variasi yang ada dari purata, atau sejauh mana nilai -nilai biasanya "menyimpang" dari purata (purata). Varians atau sisihan sifar sifar menunjukkan bahawa semua nilai adalah sama.
Varians adalah min dari kuadrat penyimpangan (i.e., perbezaan nilai dari min), dan sisihan piawai adalah akar kuadrat dari varians itu. Sisihan piawai digunakan untuk mengenal pasti outlier dalam data.
Carta Perbandingan
Perbezaan - Persamaan -| Sisihan piawai | Varians | |
|---|---|---|
| Formula matematik | Akar varians persegi | Purata kuadrat penyimpangan setiap nilai dari min dalam sampel. |
| Simbol | Sigma Surat Yunani - σ | Tiada simbol khusus; dinyatakan dari segi sisihan piawai atau nilai lain. |
| Nilai berhubung dengan set data yang diberikan | Skala yang sama seperti nilai dalam set data yang diberikan; oleh itu, dinyatakan dalam unit yang sama. | Skala lebih besar daripada nilai dalam set data yang diberikan; tidak dinyatakan dalam unit yang sama dengan nilai -nilai itu sendiri. |
| Adalah nilai negatif atau positif? | Sentiasa tidak negatif | Sentiasa tidak negatif |
| Permohonan dunia nyata | Pensampelan penduduk; mengenal pasti outliers | Formula statistik, kewangan. |
Konsep penting
- Bermaksud: Purata semua nilai dalam set data (tambahkan semua nilai dan bahagikan jumlahnya dengan bilangan nilai).
- Penyimpangan: Jarak setiap nilai dari min. Sekiranya min ialah 3, nilai 5 mempunyai sisihan 2 (tolak min dari nilai). Penyimpangan boleh positif atau negatif.
Simbol
Formula untuk sisihan piawai dan varians sering dinyatakan menggunakan:
- x̅ = min, atau purata, semua titik data dalam masalah
- X = titik data individu
- N = bilangan mata dalam set data
- Σ = jumlah [dataran penyimpangan]
Formula
Varians satu set n Nilai -nilai yang sama boleh ditulis sebagai:
Penyimpangan piawai adalah akar kuadrat varians:
Formula dengan huruf Yunani mempunyai cara untuk mencari yang menakutkan, tetapi ini kurang rumit daripada nampaknya. Untuk meletakkannya dalam langkah mudah:
- Cari purata semua titik data
- Ketahui sejauh mana setiap titik jauh dari purata (ini adalah sisihan)
- persegi setiap sisihan (i.e. perbezaan setiap nilai dari min)
- Bahagikan jumlah kuadrat dengan bilangan mata.
Yang memberikan varians. Ambil akar kuadrat varians untuk mencari sisihan piawai.
Video yang sangat baik ini dari Khan Academy menerangkan konsep varians dan sisihan piawai:
Contoh
Katakan set data termasuk ketinggian enam dandelions: 3 inci, 4 inci, 5 inci, 4 inci, 11 inci, dan 6 inci.
Pertama, cari maksud titik data: (3 + 4 + 5 + 4 + 11 + 7) / 6 = 5.5
Jadi ketinggian min ialah 5.5 inci. Sekarang kita memerlukan penyimpangan, jadi kita dapati perbezaan setiap tumbuhan dari min: -2.5, -1.5, -.5, -1.5, 5.5, 1.5
Sekarang persegi setiap penyimpangan dan cari jumlah mereka: 6.25 + 2.25 + .25 + 2.25 + 30.25 + 2.25 = 43.5
Sekarang bahagikan jumlah kuadrat dengan bilangan titik data, dalam hal ini tumbuhan: 43.5/6 = 7.25
Jadi varians set data ini ialah 7.25, yang merupakan nombor yang cukup sewenang -wenang. Untuk mengubahnya menjadi pengukuran dunia nyata, ambil akar kuadrat 7.25 untuk mencari sisihan piawai dalam inci.
Sisihan piawai adalah kira -kira 2.69 inci. Itu bermaksud bahawa untuk sampel, mana -mana dandelion dalam 2.69 inci dari min (5.5 inci) adalah 'normal'.
Mengapa persegi penyimpangan?
Penyimpangan dikelilingi untuk mengelakkan nilai negatif (penyimpangan di bawah min) daripada membatalkan nilai positif. Ini berfungsi kerana bilangan negatif kuasa dua menjadi nilai positif. Sekiranya anda mempunyai data mudah yang ditetapkan dengan penyimpangan dari purata +5, +2, -1, dan -6, jumlah penyimpangan akan keluar sebagai sifar jika nilai -nilai tidak dikuap (i.e. 5 + 2 - 1 - 6 = 0).
Aplikasi dunia sebenar
Varians dinyatakan sebagai penyebaran matematik. Oleh kerana ia adalah nombor sewenang-wenangnya berbanding dengan pengukuran asal set data, sukar untuk memvisualisasikan dan memohon dalam pengertian dunia nyata. Mencari varians biasanya hanya langkah terakhir sebelum mencari sisihan piawai. Nilai varians kadang -kadang digunakan dalam formula kewangan dan statistik.
Sisihan piawai, yang dinyatakan dalam unit asal set data, jauh lebih intuitif dan lebih dekat dengan nilai -nilai set data asal. Ia paling sering digunakan untuk menganalisis demografi atau sampel penduduk untuk mendapatkan rasa apa yang normal dalam populasi.
Mencari Outliers
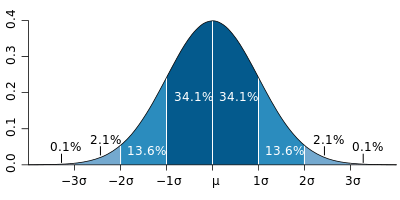Pengedaran normal (lengkung loceng) dengan band yang sepadan dengan 1σ Dalam taburan normal, kira -kira 68% penduduk (atau nilai) jatuh dalam 1 sisihan piawai (1σ) min dan kira -kira 94% jatuh dalam 2σ. Nilai yang berbeza dari min oleh 1.7σ atau lebih biasanya dianggap sebagai penyerang.
Dalam amalan, sistem kualiti seperti Six Sigma cuba mengurangkan kadar kesilapan supaya kesilapan menjadi lebih baik. Istilah "Proses Six Sigma" berasal dari tanggapan bahawa jika seseorang mempunyai enam sisihan piawai antara proses proses dan had spesifikasi terdekat, praktikalnya tidak ada item yang gagal memenuhi spesifikasi.[1]
Sampel sisihan piawai
Dalam aplikasi dunia sebenar, set data yang digunakan biasanya mewakili sampel penduduk, bukannya keseluruhan populasi. Formula yang sedikit diubahsuai digunakan jika kesimpulan seluruh penduduk akan diambil dari sampel separa.
'Sisihan piawai sampel' digunakan jika semua yang anda miliki adalah sampel, tetapi anda ingin membuat pernyataan mengenai sisihan piawai penduduk yang mana sampel ditarik
Satu-satunya cara formula sisihan piawai sampel berbeza dari formula sisihan piawai ialah "-1" dalam penyebut.
Menggunakan contoh dandelion, formula ini diperlukan jika kita mencontohi hanya 6 dandelions, tetapi ingin menggunakan sampel itu untuk menyatakan sisihan piawai untuk seluruh bidang dengan beratus -ratus dandelions.
Jumlah dataran kini dibahagikan dengan 5 bukannya 6 (n - 1), yang memberikan varians 8.7 (bukan 7.25), dan sisihan piawai sampel 2.95 inci, bukan 2.69 inci untuk sisihan piawai asal. Perubahan ini digunakan untuk mencari margin ralat dalam sampel (9% dalam kes ini).