Perbezaan antara bulatan dan sfera
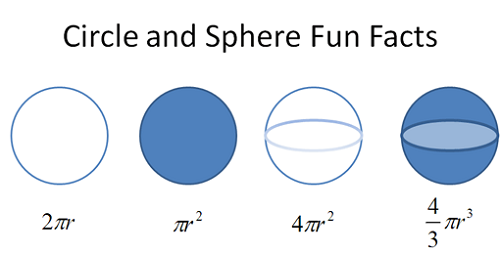
- 1520
- 105
- Ricardo Koelpin IV
Bumi di mana kita hidup dapat mengingatkan kita tentang bulatan, walaupun tidak sepenuhnya sempurna, dan kawasan 'di mana penduduk manusia terletak, dalam kes ini, dapat dikenal pasti dengan sfera. Oleh itu geometri bulatan dan sfera mempunyai aplikasi luas dalam setiap bidang sains, bermula dari, sebagai contoh - dalam geografi, geologi dan geodesy. Bentuk sfera sememangnya boleh didapati di pelbagai tempat di alam semula jadi, dan kerana rasa ingin tahu manusia, ada keperluan untuk keterangan mereka.
Apa itu bulatan?
Garis bulat adalah satu set mata dalam satah dengan harta yang semua titik garis itu berada pada jarak yang sama r dari titik tetap satah yang dipanggil pusat garis bulat. Setiap baris yang menghubungkan pusat dengan beberapa titik garis bulat dipanggil jejari, dan bilangan r adalah panjang jejari garis pekeliling itu. Dalam kesusasteraan istilah bulatan, mungkin, paling sering digunakan. Bulatan adalah kes khas elips. Ellipse boleh ditakrifkan sebagai angka geometri titik dalam satah dengan jumlah jarak yang tetap antara dua titik tetap. Sekiranya berlaku dua mata ini (pusat dan fokus) adalah sama. Diketahui bahawa setiap bulatan mempunyai set tiga mata unik yang tidak terletak di arah yang sama. Titik -titik ini menentukan tepi segitiga, dan pusat bulatan yang dilampirkan segitiga ini berada di bahagian silang garis biseksi. Jarak dari pusat ke mana -mana tiga titik yang diberikan ialah jejari bulatan. Satu lagi cara untuk menentukan bulatan melalui tiga mata adalah untuk menulis persamaan bentuk umum bulatan, dalam bentuk kanonik (standard) atau titik-lereng, untuk memasukkan koordinat mata yang diberikan dan untuk menyelesaikan sistem. Kawasan bulatan yang diberikan dengan radius r adalah sama dengan πr2.
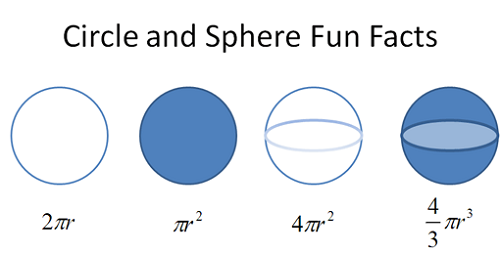
Apa itu sfera?
Ruang boleh dilihat sebagai satu set mata yang disebut elemen ruang. Bola adalah badan geometri yang merupakan subset ruang. Ia adalah satu set titik satah yang berada pada jarak tertentu (panjang) dari titik tetap o. Titik o adalah pusat sfera, dan panjang yang menghubungkan pusat dengan titik paling jauh dari sfera dipanggil jejari. Diameter adalah garis yang menghubungkan dua titik kelebihan yang paling jauh (garis lurus terpanjang) dari sfera dan melewati pusatnya. Lingkaran yang dibentuk oleh persimpangan sfera dan pesawat yang melewati pusat sfera dipanggil lingkaran besar sfera. Semua bulatan lain yang dibentuk oleh persimpangan satah dan sfera dipanggil bulatan kecil dari sfera. Melalui setiap set tiga titik sfera, hanya ada satu bulatan yang dimiliki olehnya.
- Kawasan sfera ialah 4πr2;
- Jumlah sfera ialah 4/3πr3;
Perbezaan antara bulatan dan sfera
- Definisi
Bulatan adalah garis melengkung tertutup. Setiap titik pada garis melengkung ini berada pada jarak yang sama dari titik fokus (pusat) bulatan. Lokus titik yang berada pada panjang tetap dari titik lain dikenali sebagai bulatan. Titik tetap adalah pusat bulatan, dan panjang antara kedua -dua titik ini jejari. Begitu juga, sfera juga dicirikan sebagai lokus titik yang berada pada jarak yang tetap dari titik tetap - namun dalam ruang tiga dimensi. Secara ringkas - bulatan adalah objek bulat dalam satah, sementara sfera adalah objek bulat di ruang.
- Formula
Bulatan, sebagai angka dua dimensi hanya mempunyai kawasan - πr2. Sfera, sebaliknya, sebagai angka tiga dimensi (objek) mempunyai kawasan - 4πr2 dan kelantangan - 4/3πr3.
- Contoh
Secara semulajadi, bulatan dan sfera adalah angka yang boleh dijumpai di sekeliling kita. Walaupun contoh dunia lingkaran tidak wujud kerana tidak ada objek lebar sifar dalam realiti - beberapa objek dapat digunakan untuk menggambarkannya - seperti roda, CD, duit syiling. Contoh sfera mungkin lebih mudah dicari - bola tenis, planet, oren, glob dll.
Bulatan vs. Sfera
| Bulatan | Sfera |
| objek bulat dalam kapal terbang | objek bulat di ruang |
| Dua dimensi (angka) | tiga dimensi (objek) |
| Hanya kawasan yang boleh dikira | Pengiraan termasuk kedua -dua kawasan dan kelantangan |
Ringkasan
- Bulatan dan sfera mempunyai simetri yang sempurna di sekitar pusat mereka. Semua titik bulatan, dan titik paling jauh dari sfera berada pada jarak tetap dari titik fokus (pusat). Walau bagaimanapun, terdapat perbezaan seperti bulatan yang dua dimensi, sementara sfera adalah objek tiga dimensi. Jarak antara titik yang paling jauh dipanggil diameter (dan dua kali ganda jejari).
- Bulatan mempunyai kawasan yang boleh dikira dengan formula - πr2. Sfera bersama dengan kawasan (dikira dengan formula 4πr2) mempunyai jumlah yang sama dengan 4/3πr3.
- Contoh kehidupan sebenar bulatan tidak dapat dijumpai sebagai lingkaran wujud sebagai konsep dua dimensi - ia hanya mendapat panjang dan ketinggian dan tiada lebar. Walau bagaimanapun, objek tertentu boleh menyerupai bulatan - cookies, pizza, tayar ... contoh objek seperti sfera adalah softball, guli, atom, epal dan sebagainya.

