Perbezaan antara acara yang saling eksklusif dan bebas
- 2162
- 99
- Ricardo Koelpin IV
 Kebarangkalian adalah konsep matematik, yang kini menjadi disiplin sepenuhnya dan merupakan bahagian penting dalam statistik. Percubaan rawak dalam kebarangkalian adalah prestasi yang menghasilkan hasil tertentu, semata -mata berdasarkan peluang. Hasil percubaan rawak dipanggil peristiwa. Dalam kebarangkalian, terdapat pelbagai jenis peristiwa, seperti yang mudah, kompaun, saling eksklusif, menyeluruh, bebas, bergantung, sama, dan sebagainya. Apabila peristiwa tidak dapat berlaku pada masa yang sama, mereka dipanggil saling eksklusif
Kebarangkalian adalah konsep matematik, yang kini menjadi disiplin sepenuhnya dan merupakan bahagian penting dalam statistik. Percubaan rawak dalam kebarangkalian adalah prestasi yang menghasilkan hasil tertentu, semata -mata berdasarkan peluang. Hasil percubaan rawak dipanggil peristiwa. Dalam kebarangkalian, terdapat pelbagai jenis peristiwa, seperti yang mudah, kompaun, saling eksklusif, menyeluruh, bebas, bergantung, sama, dan sebagainya. Apabila peristiwa tidak dapat berlaku pada masa yang sama, mereka dipanggil saling eksklusif
Sebaliknya, jika setiap peristiwa tidak terjejas oleh peristiwa lain, mereka dipanggil peristiwa bebas. Ambil bacaan penuh artikel yang dibentangkan di bawah untuk mempunyai pemahaman yang lebih baik tentang perbezaan antara peristiwa yang saling eksklusif dan bebas.
Kandungan: Acara yang saling eksklusif vs Acara Bebas
- Carta Perbandingan
- Definisi
- Perbezaan utama
- Kesimpulan
Carta Perbandingan
| Asas untuk perbandingan | Peristiwa yang saling eksklusif | Peristiwa bebas |
|---|---|---|
| Makna | Dua peristiwa dikatakan saling eksklusif, apabila kejadian mereka tidak serentak. | Dua peristiwa dikatakan bebas, apabila berlakunya satu peristiwa tidak dapat mengawal berlakunya yang lain. |
| Pengaruh | Kejadian satu peristiwa akan mengakibatkan tidak terjejas yang lain. | Kejadian satu peristiwa tidak akan mempunyai pengaruh terhadap kejadian yang lain. |
| Formula matematik | P (a dan b) = 0 | P (a dan b) = p (a) p (b) |
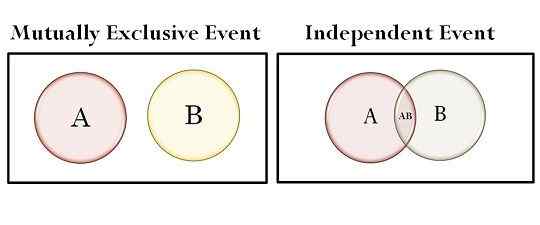
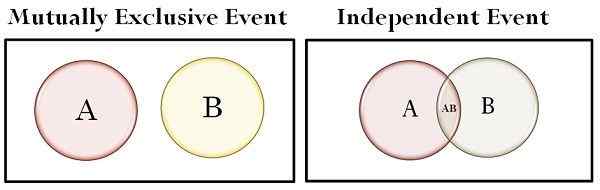
| Set di gambarajah Venn | Tidak bertindih | Bertindih |
Definisi acara yang saling eksklusif
Acara eksklusif yang saling eksklusif adalah yang tidak dapat berlaku serentak, i.e. di mana berlakunya satu peristiwa mengakibatkan tidak terjejas peristiwa lain. Acara sedemikian tidak boleh berlaku pada masa yang sama. Oleh itu, kejadian satu peristiwa membuat kejadian lain yang mustahil. Ini juga dikenali sebagai peristiwa disjoint.
Mari kita ambil contoh melemparkan duit syiling, di mana hasilnya sama ada kepala atau ekor. Kedua -dua kepala dan ekor tidak dapat berlaku secara serentak. Ambil contoh lain, katakan jika syarikat mahu membeli jentera, yang mana ia mempunyai dua pilihan mesin a dan b. Mesin yang kos efektif dan produktiviti lebih baik, akan dipilih. Penerimaan Mesin A akan secara automatik mengakibatkan penolakan mesin B dan sebaliknya.
Definisi acara bebas
Seperti namanya, peristiwa bebas adalah peristiwa, di mana kebarangkalian satu peristiwa tidak mengawal kebarangkalian kejadian lain. Yang berlaku atau tidak ada peristiwa sedemikian tidak sama sekali tidak memberi kesan kepada kejadian yang tidak berlaku atau tidak ada yang lain. Produk kebarangkalian berasingan mereka sama dengan kebarangkalian bahawa kedua -dua peristiwa akan berlaku.
Mari kita ambil contoh, anggap jika duit syiling dilemparkan dua kali, ekor dalam peluang pertama dan ekor di tempat kedua, peristiwa -peristiwa itu bebas. Satu lagi contoh untuk ini, anggap jika dadu dilancarkan dua kali, 5 dalam peluang pertama dan 2 di tempat kedua, peristiwa itu bebas.
Perbezaan utama antara acara yang saling eksklusif dan bebas
Perbezaan yang signifikan antara peristiwa yang saling eksklusif dan bebas dijelaskan seperti di bawah:
- Peristiwa yang saling eksklusif adalah peristiwa -peristiwa ketika kejadian mereka tidak serentak. Apabila berlakunya satu peristiwa tidak dapat mengawal berlakunya yang lain, peristiwa tersebut dipanggil peristiwa bebas.
- Dalam peristiwa yang saling eksklusif, berlakunya satu peristiwa akan mengakibatkan tidak terjejas yang lain. Sebaliknya, dalam peristiwa bebas, kejadian satu peristiwa tidak akan mempunyai pengaruh terhadap kejadian yang lain.
- Peristiwa eksklusif yang saling eksklusif diwakili secara matematik sebagai p (a dan b) = 0 manakala peristiwa bebas diwakili sebagai p (a dan b) = p (a) p (b).
- Dalam gambarajah Venn, set tidak bertindih antara satu sama lain, dalam hal peristiwa yang saling eksklusif sementara jika kita bercakap tentang peristiwa bebas set tumpang tindih.
Kesimpulan
Oleh itu, dengan perbincangan di atas, agak jelas bahawa kedua -dua peristiwa itu tidak sama. Lebih -lebih lagi, ada satu perkara yang perlu diingat, dan itu adalah jika peristiwa saling eksklusif, maka ia tidak boleh bebas dan sebaliknya. Jika dua peristiwa A dan B saling eksklusif, maka mereka boleh dinyatakan sebagai P (AUB) = P (A)+P (B) manakala jika pembolehubah yang sama bebas maka mereka boleh dinyatakan sebagai P (A∩B) = P (a) p (b).

