Perbezaan antara parabola dan hiperbola

Parabola vs hyperbola

Parabola dan hyperbola adalah dua bahagian yang berlainan dari kerucut. Kita dapat menangani perbezaan mereka dalam penjelasan matematik atau menangani perbezaan dengan cara yang sangat mudah yang bukan hanya ahli matematik tetapi semua orang dapat memahami. Artikel ini akan cuba menjelaskan perbezaan di antara mereka dengan cara yang sangat mudah.
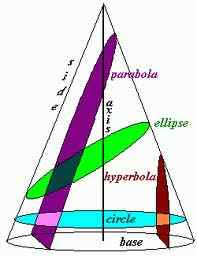
Pertama sekali, apabila angka pepejal, yang dalam kes ini adalah kerucut, dipotong oleh satah, bahagian yang diperolehi dipanggil bahagian konik. Bahagian konik boleh menjadi bulatan, elips, hiperbola, dan parabola bergantung kepada sudut persimpangan antara paksi kon dan pesawat. Kedua -dua parabola dan hiperbola adalah lengkung terbuka yang bermaksud bahawa lengan atau cawangan lengkung terus menjadi tak terhingga; mereka tidak lekuk tertutup seperti bulatan atau elips.

Parabola
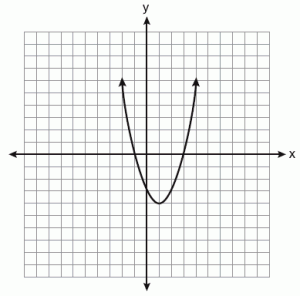
Parabola adalah lengkung yang diperoleh ketika pesawat memotong selari dengan sisi kerucut. Dalam parabola, garis yang melalui tumpuan dan tegak lurus ke directrix dipanggil "paksi simetri."Apabila parabola dipintas oleh titik pada" paksi simetri, "ia disebut sebagai" puncak."Semua parabola dibentuk secara identik kerana mereka dipotong pada sudut tertentu. Ia dicirikan oleh eksentrik "1."Inilah sebab mengapa mereka semua bentuk yang sama tetapi boleh menjadi saiz yang berbeza.

Parabola diberikan oleh persamaan y2 = x
Apabila satu set mata yang hadir dalam satah adalah sama dari Directrix, garis lurus yang diberikan, dan sama dengan tumpuan, titik tertentu yang ditetapkan, ia dipanggil parabola.
Parabola mempunyai banyak aplikasi praktikal. Mereka digunakan untuk merancang jalan peluru berpandu, reflektor lampu kereta, teleskop, penerima radar, dan hidangan satelit.

Hyperbola

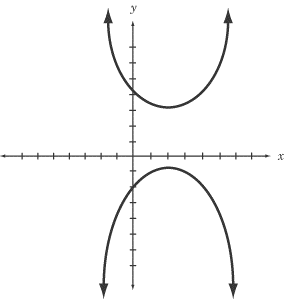
Hyperbola adalah lengkung yang diperoleh apabila pesawat memotong hampir selari dengan paksi. Hyperbolas tidak sama dengan bentuk kerana terdapat banyak sudut antara paksi dan pesawat. "Vertices" adalah titik pada kedua -dua lengan yang paling dekat; sedangkan segmen garis yang menghubungkan lengan dipanggil "paksi utama."
Di Parabola, kedua -dua lengan lengkung, juga dipanggil cawangan, menjadi selari antara satu sama lain. Dalam hiperbola, kedua -dua lengan atau lengkung tidak selari. Pusat hiperbola adalah titik tengah paksi utama.

Hyperbola diberikan oleh persamaan xy = 1

Apabila perbezaan jarak antara satu set mata yang hadir dalam satah ke dua foci tetap atau titik adalah pemalar positif, ia dipanggil hyperbola.

Ringkasan:
Apabila satu set mata yang hadir dalam satah adalah sama dari Directrix, garis lurus yang diberikan, dan sama dengan tumpuan, titik tertentu yang ditetapkan, ia dipanggil parabola. Apabila perbezaan jarak antara satu set mata yang hadir dalam satah ke dua foci tetap atau titik adalah pemalar positif, ia dipanggil hyperbola.
Semua parabola adalah bentuk yang sama tidak kira apa saiznya; Semua hiperbola adalah pelbagai bentuk
Parabola diberikan oleh persamaan y2 = x; hiperbola diberikan oleh persamaan xy = 1
Dalam parabola kedua -dua lengan menjadi selari antara satu sama lain sedangkan dalam hiperbola mereka tidak.