Perbezaan antara varians dan sisihan piawai

- 2732
- 451
- Stuart Kovacek
 Penyebaran menunjukkan sejauh mana pemerhatian menyimpang dari ukuran kecenderungan pusat yang sesuai. Langkah penyebaran jatuh ke dalam dua kategori i.e. ukuran penyebaran mutlak dan ukuran penyebaran relatif. Varians dan sisihan piawai adalah dua jenis ukuran mutlak kebolehubahan; yang menerangkan bagaimana pemerhatian tersebar di sekitar maksudnya. Varians tidak lain hanyalah purata kuadrat penyimpangan,
Penyebaran menunjukkan sejauh mana pemerhatian menyimpang dari ukuran kecenderungan pusat yang sesuai. Langkah penyebaran jatuh ke dalam dua kategori i.e. ukuran penyebaran mutlak dan ukuran penyebaran relatif. Varians dan sisihan piawai adalah dua jenis ukuran mutlak kebolehubahan; yang menerangkan bagaimana pemerhatian tersebar di sekitar maksudnya. Varians tidak lain hanyalah purata kuadrat penyimpangan,
Tidak seperti, sisihan piawai adalah akar kuadrat nilai berangka yang diperoleh semasa mengira varians. Ramai orang membezakan dua konsep matematik ini. Oleh itu, artikel ini membuat percubaan untuk memberi penjelasan mengenai perbezaan penting antara varians dan sisihan piawai.
Kandungan: Varians vs sisihan piawai
- Carta Perbandingan
- Definisi
- Perbezaan utama
- Ilustrasi
- Persamaan
- Kesimpulan
Carta Perbandingan
| Asas untuk perbandingan | Varians | Sisihan piawai |
|---|---|---|
| Makna | Varians adalah nilai berangka yang menggambarkan kebolehubahan pemerhatian dari aritmetiknya. | Sisihan piawai adalah ukuran penyebaran pemerhatian dalam set data. |
| Apa itu? | Ia adalah purata penyimpangan kuasa dua. | Ia adalah sisihan persegi min akar. |
| Dilabelkan sebagai | Sigma-kuadrat (σ^2) | Sigma (σ) |
| Dinyatakan dalam | Unit Squared | Unit yang sama dengan nilai dalam set data. |
| Menunjukkan | Sejauh mana individu dalam kumpulan tersebar. | Berapa banyak pemerhatian set data berbeza dari maksudnya. |
Definisi varians
Dalam statistik, varians ditakrifkan sebagai ukuran kebolehubahan yang mewakili sejauh mana ahli kumpulan tersebar. Ia mendapati tahap purata yang mana setiap pemerhatian berbeza dari min. Apabila varians set data adalah kecil, ia menunjukkan kedekatan data titik kepada min sedangkan nilai varians yang lebih besar mewakili bahawa pemerhatian sangat tersebar di sekitar aritmetik dan antara satu sama lain.
Untuk data yang tidak dikelaskan: 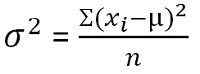
Untuk pengedaran frekuensi dikumpulkan: 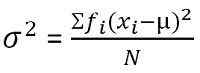
Definisi sisihan piawai
Sisihan piawai adalah ukuran yang mengukur jumlah penyebaran pemerhatian dalam dataset. Penyimpangan piawai yang rendah adalah penunjuk kedekatan skor kepada min aritmetik dan sisihan piawai yang tinggi mewakili; Skor disebarkan ke atas nilai yang lebih tinggi.
Untuk data yang tidak dikelaskan: 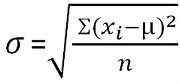 Untuk pengedaran frekuensi dikumpulkan:
Untuk pengedaran frekuensi dikumpulkan: 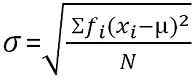
Perbezaan utama antara varians dan sisihan piawai
Perbezaan antara sisihan piawai dan varians boleh ditarik dengan jelas berdasarkan alasan berikut:
- Varians adalah nilai berangka yang menggambarkan kebolehubahan pemerhatian dari aritmetiknya. Sisihan piawai adalah ukuran penyebaran pemerhatian dalam set data berbanding dengan maksudnya.
- Varians hanyalah purata penyimpangan kuasa dua. Sebaliknya, sisihan piawai adalah sisihan persegi min akar.
- Varians dilambangkan oleh sigma-kuadrat (σ2) manakala sisihan piawai dilabelkan sebagai sigma (σ).
- Varians dinyatakan dalam unit persegi yang biasanya lebih besar daripada nilai dalam dataset yang diberikan. Berbanding dengan sisihan piawai yang dinyatakan dalam unit yang sama seperti nilai dalam set data.
- Varians mengukur sejauh mana individu dalam kumpulan tersebar dalam set data dari purata. Sebaliknya, sisihan piawai mengukur berapa banyak pemerhatian set data berbeza dari maksudnya.
Ilustrasi
Tanda yang dijaringkan oleh pelajar dalam lima mata pelajaran masing -masing adalah 60, 75, 46, 58 dan 80. Anda mesti mengetahui sisihan piawai dan varians.
Pertama sekali, anda mesti mengetahui maksudnya,
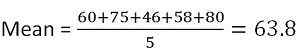
Jadi tanda purata (min) adalah 63.8
Sekarang hitung varians
| X | A | (x-a) | (X-a)^2 |
|---|---|---|---|
| 60 | 63.8 | -3.8 | 14.44 |
| 75 | 63.8 | 11.2 | 125.44 |
| 46 | 63.8 | -17.8 | 316.84 |
| 58 | 63.8 | 5.8 | 33.64 |
| 80 | 63.8 | 16.2 | 262.44 |
Di mana, x = pemerhatian
A = Maksud aritmetik
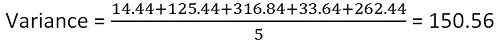 Jadi varians ialah 150.56
Jadi varians ialah 150.56
Dan sisihan piawai adalah - 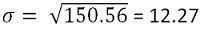
Persamaan
- Kedua -dua varians dan sisihan piawai sentiasa positif.
- Jika semua pemerhatian dalam set data adalah sama, maka sisihan piawai dan varians akan menjadi sifar.
Kesimpulan
Kedua -duanya adalah istilah statistik asas, yang memainkan peranan penting dalam sektor yang berbeza. Sisihan piawai lebih disukai daripada min kerana ia dinyatakan dalam unit yang sama seperti pengukuran sementara varians dinyatakan dalam unit yang lebih besar daripada set data yang diberikan.

