Perbezaan antara ujian t dan z

- 4837
- 293
- Dr. Anthony Turcotte
 Ujian t merujuk kepada ujian hipotesis univariat berdasarkan t-statistik, di mana min diketahui, dan varians penduduk dianggarkan dari sampel. Sebaliknya, Z-TEST juga merupakan ujian univariat yang berdasarkan taburan normal standard.
Ujian t merujuk kepada ujian hipotesis univariat berdasarkan t-statistik, di mana min diketahui, dan varians penduduk dianggarkan dari sampel. Sebaliknya, Z-TEST juga merupakan ujian univariat yang berdasarkan taburan normal standard.
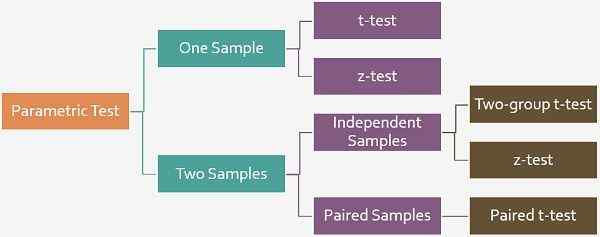
Secara ringkas, hipotesis merujuk kepada anggapan yang akan diterima atau ditolak. Terdapat dua prosedur ujian hipotesis, i.e. Ujian parametrik dan ujian bukan parametrik, di mana ujian parametrik didasarkan pada fakta bahawa pembolehubah diukur pada skala selang, sedangkan dalam ujian bukan parametrik, yang sama dianggap diukur pada skala ordinal. Sekarang, dalam ujian parametrik, terdapat dua jenis ujian, ujian t dan ujian z.
Artikel ini akan memberi anda pemahaman tentang perbezaan antara ujian t dan Z secara terperinci.
Kandungan: ujian t vs z-ujian
- Carta Perbandingan
- Definisi
- Perbezaan utama
- Kesimpulan
Carta Perbandingan
| Asas untuk perbandingan | Ujian t | Z-TEST |
|---|---|---|
| Makna | Ujian t merujuk kepada jenis ujian parametrik yang digunakan untuk mengenal pasti, bagaimana cara dua set data berbeza antara satu sama lain apabila varians tidak diberikan. | Z-Test membayangkan ujian hipotesis yang menentukan jika cara dua dataset berbeza antara satu sama lain apabila varians diberikan. |
| Berdasarkan | Pengagihan Pelajar-T | Taburan normal |
| Varians penduduk | Tidak diketahui | Dikenali |
| Saiz sampel | Kecil | Besar |
Definisi ujian t
Ujian t adalah ujian hipotesis yang digunakan oleh penyelidik untuk membandingkan cara penduduk untuk pembolehubah, diklasifikasikan kepada dua kategori bergantung pada pemboleh ubah selang kurang daripada. Lebih tepat lagi, ujian t digunakan untuk mengkaji bagaimana cara yang diambil dari dua sampel bebas berbeza.
Ujian t berikut pengedaran t, yang sesuai apabila saiz sampel kecil, dan sisihan piawai penduduk tidak diketahui. Bentuk pengedaran t sangat terjejas oleh tahap kebebasan. Tahap kebebasan membayangkan bilangan pemerhatian bebas dalam satu set pemerhatian tertentu.
Andaian ujian t:
- Semua titik data adalah bebas.
- Saiz sampel kecil. Umumnya, saiz sampel melebihi 30 unit sampel dianggap besar, jika tidak kecil tetapi tidak sepatutnya kurang daripada 5, untuk memohon ujian t.
- Nilai sampel hendaklah diambil dan direkodkan dengan tepat.
Statistik ujian adalah:
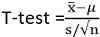
x ̅is maksud sampel
s ialah sisihan piawai sampel
n ialah saiz sampel
μ adalah maksud penduduk
Ujian t berpasangan: Ujian statistik yang digunakan apabila kedua -dua sampel itu bergantung dan pemerhatian berpasangan diambil.
Definisi Z-Test
Ujian Z merujuk kepada analisis statistik univariat yang digunakan untuk menguji hipotesis bahawa perkadaran dari dua sampel bebas sangat berbeza. Ia menentukan sejauh mana titik data jauh dari min set data, dalam sisihan piawai.
Penyelidik mengamalkan ujian Z, apabila varians populasi diketahui, pada dasarnya, apabila terdapat saiz sampel yang besar, varians sampel dianggap kira-kira sama dengan varians penduduk. Dengan cara ini, diandaikan diketahui, walaupun pada hakikatnya hanya data sampel yang tersedia dan ujian normal dapat digunakan.
Andaian Z-Test:
- Semua pemerhatian sampel adalah bebas
- Saiz sampel hendaklah lebih dari 30.
- Pengagihan z adalah normal, dengan sifar min dan varians 1.
Statistik ujian adalah:
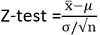
x ̅is maksud sampel
σ adalah sisihan piawai penduduk
n ialah saiz sampel
μ adalah maksud penduduk
Perbezaan utama antara ujian t dan z-z
Perbezaan antara ujian t dan z boleh ditarik dengan jelas atas dasar berikut:
- Ujian t dapat difahami sebagai ujian statistik yang digunakan untuk membandingkan dan menganalisis sama ada cara kedua-dua penduduknya berbeza antara satu sama lain atau tidak apabila sisihan piawai tidak diketahui. Sebaliknya, ujian z adalah ujian parametrik, yang digunakan apabila sisihan piawai diketahui, untuk menentukan, jika cara kedua-dua dataset berbeza antara satu sama lain.
- Ujian t didasarkan pada pengagihan t pelajar. Sebaliknya, Z-Test bergantung pada andaian bahawa pengedaran cara sampel adalah normal. Pengagihan T dan pengedaran normal kedua-dua pelajar kelihatan sama, kerana kedua-duanya adalah simetri dan berbentuk loceng. Walau bagaimanapun, mereka berbeza dalam erti kata bahawa dalam pengedaran T, terdapat ruang yang kurang di tengah dan lebih banyak di ekor.
- Salah satu syarat penting untuk mengadopsi t-ujian ialah varians penduduk tidak diketahui. Sebaliknya, varians penduduk harus diketahui atau dianggap diketahui dalam hal ujian z.
- Z-ujian digunakan apabila saiz sampel besar, i.e. n> 30, dan ujian t sesuai apabila saiz sampel kecil, dalam erti kata bahawa n < 30.
Kesimpulan
Secara besar, ujian t dan z-ujian hampir sama, tetapi syarat-syarat untuk permohonan mereka berbeza, yang bermaksud bahawa ujian t sesuai apabila saiz sampel tidak melebihi 30 unit. Walau bagaimanapun, jika lebih daripada 30 unit, ujian z mesti dilakukan. Begitu juga, ada syarat -syarat lain, yang menjelaskan bahawa ujian mana yang akan dilakukan dalam keadaan tertentu.

