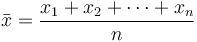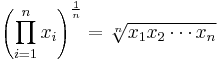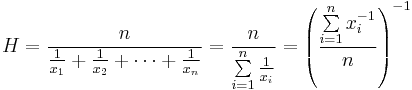Min vs. Median
- 2437
- 653
- Ms. Lee Bechtelar
Maksudnya (atau purata) dan median adalah istilah statistik yang mempunyai peranan yang agak serupa dari segi pemahaman kecenderungan pusat satu set skor statistik. Walaupun purata secara tradisinya menjadi ukuran popular titik pertengahan dalam sampel, ia mempunyai kelemahan yang dipengaruhi oleh mana-mana nilai tunggal yang terlalu tinggi atau terlalu rendah berbanding dengan sampel yang lain. Inilah sebabnya mengapa median kadang -kadang diambil sebagai ukuran yang lebih baik dari titik pertengahan.
Carta Perbandingan
| Maksudnya | Median | |
|---|---|---|
| Definisi | Maksudnya ialah purata aritmetik satu set nombor, atau pengedaran. Ia adalah ukuran kecenderungan pusat yang paling biasa digunakan dari satu set nombor. | Median digambarkan sebagai nilai angka yang memisahkan separuh sampel yang lebih tinggi, populasi, atau taburan kebarangkalian, dari bahagian bawah. |
| Kebolehgunaan | Maksudnya digunakan untuk pengagihan biasa. | Median biasanya digunakan untuk pengagihan miring. |
| Kaitan dengan set data | Maksudnya bukan alat yang mantap kerana ia sebahagian besarnya dipengaruhi oleh outlier. | Median lebih sesuai untuk pengagihan miring untuk memperoleh kecenderungan pusat kerana ia lebih mantap dan masuk akal. |
| Cara mengira | Purata dikira dengan menambahkan semua nilai dan membahagikan skor tersebut dengan bilangan nilai. | Median adalah bilangan yang terdapat di tengah -tengah tepat set nilai. Median boleh dikira dengan menyenaraikan semua nombor dalam urutan menaik dan kemudian mencari nombor di tengah pengedaran tersebut. |
Definisi min dan median
Dalam matematik dan statistik, min atau Maksud aritmetik senarai nombor adalah jumlah keseluruhan senarai yang dibahagikan dengan bilangan item dalam senarai. Semasa melihat pengagihan simetri, min mungkin langkah terbaik untuk mencapai kecenderungan pusat. Dalam teori kebarangkalian dan statistik, a median Adakah bilangan itu memisahkan separuh sampel yang lebih tinggi, populasi, atau taburan kebarangkalian, dari bahagian bawah.
Cara mengira
The Maksudnya atau purata mungkin kaedah yang paling biasa digunakan untuk menggambarkan kecenderungan pusat. Purata dikira dengan menambahkan semua nilai dan membahagikan skor tersebut dengan bilangan nilai. The Maksud aritmetik sampel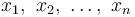 
adalah jumlah nilai sampel yang dibahagikan dengan bilangan item dalam sampel:
The Median adalah bilangan yang terdapat di tengah -tengah tepat dari set nilai. Median boleh dikira dengan menyenaraikan semua nombor dalam urutan menaik dan kemudian mencari nombor di tengah pengedaran tersebut. Ini boleh digunakan untuk senarai nombor ganjil; Sekiranya terdapat banyak pemerhatian, tidak ada nilai tengah tunggal, jadi amalan biasa untuk mengambil min dari dua nilai pertengahan.
Contoh
Mari kita katakan bahawa terdapat sembilan pelajar dalam kelas dengan skor berikut pada ujian: 2, 4, 5, 7, 8, 10, 12, 13, 83. Dalam kes ini skor purata (atau maksudnya) adalah jumlah semua skor yang dibahagikan dengan sembilan. Ini berfungsi hingga 144/9 = 16. Perhatikan bahawa walaupun 16 adalah purata aritmetik, ia diputarbelitkan oleh skor yang luar biasa tinggi 83 berbanding skor lain. Hampir semua skor pelajar di bawah purata. Oleh itu, dalam kes ini min bukan wakil yang baik dari kecenderungan pusat sampel ini.
The median, Sebaliknya, nilai yang sedemikian rupa sehingga separuh skor berada di atasnya dan separuh skor di bawah. Jadi dalam contoh ini, median adalah 8. Terdapat empat skor di bawah dan empat di atas nilai 8. Jadi 8 mewakili titik pertengahan atau kecenderungan utama sampel.
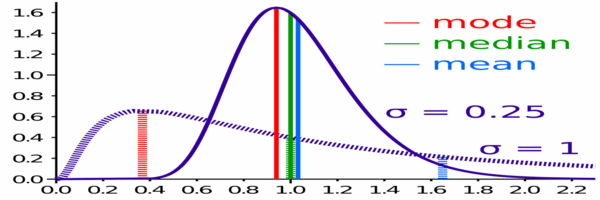Perbandingan min, median dan mod dua pengagihan log-normal dengan skewness yang berbeza. Kekurangan cara aritmetik dan median
Bermaksud bukan alat statistik yang mantap kerana ia tidak dapat digunakan untuk semua pengagihan tetapi mudah alat statistik yang paling banyak digunakan untuk memperoleh kecenderungan pusat. Sebab maksudnya tidak dapat digunakan untuk semua pengagihan adalah kerana ia mendapat dampak yang terlalu dipengaruhi oleh nilai -nilai dalam sampel yang terlalu kecil hingga terlalu besar.
Kelemahan median adalah sukar untuk mengendalikan secara teorinya. Tidak ada formula matematik yang mudah untuk mengira median.
Jenis cara lain
Terdapat banyak cara untuk menentukan kecenderungan pusat, atau purata, satu set nilai. Maksud yang dibincangkan di atas secara teknikal adalah aritmetik, dan merupakan statistik yang paling biasa digunakan untuk purata. Terdapat cara lain:
Maksud geometri
Maksud geometri ditakrifkan sebagai nakar produk dari n nombor, i.e., untuk satu set nombor x1,x2,… ,xn, Maksud geometri ditakrifkan sebagai
Cara geometri lebih baik daripada cara aritmetik untuk menerangkan pertumbuhan berkadar. Contohnya, permohonan yang baik untuk min geometri adalah mengira kadar pertumbuhan tahunan yang dikompaun (CAGR).
Maksud harmonik
Maksud harmonik adalah timbal balik min aritmetik dari timbal balik. Maksud harmonik H nombor sebenar positif x1,x2,… ,xn adalah
Permohonan yang baik untuk cara harmonik adalah apabila purata gandaan. Untuk exampe, lebih baik menggunakan maksud harmonik berwajaran apabila mengira nisbah harga pendapatan purata (P/E). Sekiranya nisbah P/E purata menggunakan aritmetik berwajaran, titik data yang tinggi mendapat berat yang lebih besar daripada titik data yang rendah.
Pythagorean bermaksud
Maksud aritmetik, maksud geometri dan harmonik bersama -sama membentuk satu set cara yang dipanggil Pythagorean bermaksud. Untuk mana -mana set nombor, maksud harmonik sentiasa terkecil dari semua cara Pythagorean, dan min aritmetik selalu menjadi yang terbesar dari 3 cara. i.e. Purata harmonik ≤ geometri min ≤ aritmetik min.
Makna lain dari kata -kata
Maksudnya boleh digunakan sebagai tokoh ucapan dan memegang rujukan sastera. Ia juga digunakan untuk menyiratkan miskin atau tidak menjadi hebat. Median, Dalam rujukan geometri, adalah garis lurus yang berlalu dari satu titik di segitiga ke pusat di seberang.