Perbezaan antara pembezaan dan integrasi

Kalkulus adalah salah satu aplikasi matematik utama yang digunakan di dunia hari ini untuk menyelesaikan pelbagai fenomena. Ia sangat bekerja dalam kajian saintifik, kajian ekonomi, kewangan, dan kejuruteraan antara disiplin lain yang memainkan peranan penting dalam kehidupan individu. Integrasi dan pembezaan adalah asas yang digunakan dalam kalkulus untuk mengkaji perubahan. Walau bagaimanapun, ramai orang, termasuk pelajar dan ulama tidak dapat menyerlahkan perbezaan antara pembezaan dan integrasi.

Apa itu pembezaan?

Pembezaan adalah istilah yang digunakan dalam kalkulus untuk merujuk kepada perubahan dalam, yang mempunyai pengalaman sifat mengenai perubahan unit dalam harta lain yang berkaitan.

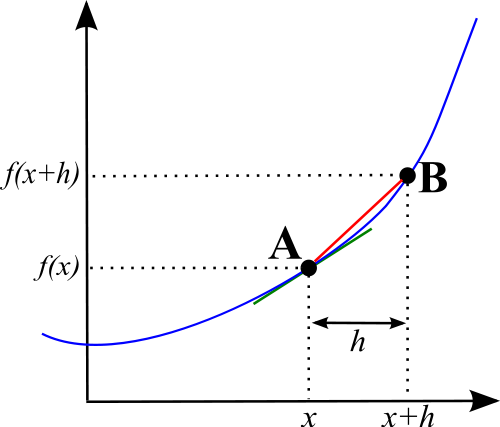
Dalam istilah lain, pembezaan membentuk ungkapan algebra yang membantu dalam pengiraan kecerunan lengkung pada titik tertentu. Penting untuk menyerlahkan bahawa lengkung mempunyai lereng mereka yang berbeza -beza pada titik tertentu tidak seperti garis lurus, yang mempunyai kecerunan yang sama sepanjang masa.

Apa itu Integrasi?

Integrasi adalah istilah yang digunakan dalam kalkulus untuk merujuk kepada formula dan prosedur mengira kawasan di bawah lengkung.

Perlu diingat bahawa graf mesti berada di bawah lengkung, yang menghasilkan pembentukan bahagian penting, yang sukar untuk mencari kawasan tidak seperti bentuk lain seperti bulatan, dataran, dan segi empat tepat, yang lebih mudah untuk mengira kawasan mereka.

Perbezaan antara pembezaan dan integrasi

1) Tujuan dan fungsi pembezaan dan integrasi

Integrasi dan pembezaan boleh dibezakan terutamanya dalam cara kedua -dua konsep digunakan dan hasil muktamad mereka. Mereka biasa mencapai jawapan yang berbeza, yang merupakan perbezaan asas. Pembezaan digunakan dalam mengira kecerunan lengkung. Lengkung tak linear mempunyai cerun yang berbeza di mana -mana titik tertentu, yang menjadikannya sukar untuk menentukan kecerunan mereka. Ekspresi algebra yang digunakan untuk menentukan perubahan yang ditanggung dari satu titik ke satu sama lain dengan unit disebut sebagai pembezaan.  Sebaliknya, integrasi adalah ungkapan algebra yang digunakan dalam mengira kawasan di bawah lengkung kerana ia bukan bentuk yang sempurna selepas kawasan mana yang dapat dikira dengan mudah.

2) bertentangan langsung

Fungsi algebra pembezaan dan integrasi adalah bertentangan antara satu sama lain, khususnya dalam aplikasi mereka. Sekiranya seseorang melakukan integrasi, dia dikatakan menunjukkan kebalikan dari pembezaan sementara jika seseorang melakukan pembezaan, dia melakukan bertentangan dengan integrasi. Sebagai contoh, integrasi dan pembezaan membentuk hubungan yang juga digambarkan apabila seseorang melakukan kuadrat nombor dan kemudian mendapati akar kuadrat hasilnya. Oleh itu, jika seseorang ingin mencari kebalikan dari nombor bersepadu, dia akan dikehendaki melakukan pembezaan nombor yang sama. Ringkasnya, integrasi adalah proses pembezaan dan sebaliknya.

3) Permohonan kehidupan sebenar untuk pembezaan dan integrasi

Dalam senario kehidupan sebenar, integrasi dan pembezaan telah didapati digunakan secara berbeza untuk setiap konsep yang digunakan dalam memberikan hasil yang berbeza. Walau bagaimanapun, adalah luar biasa untuk menyerlahkan bahawa kedua -dua pembezaan adalah konsep kalkulus penting yang menjadikan hidup mudah. Salah satu penerapan integrasi utama adalah mengira kawasan permukaan melengkung, mengira jumlah objek, dan mengira titik pusat antara fungsi lain.

Sebaliknya, konsep pembezaan digunakan dengan ketara dalam mengira halaju serta -merta dan digunakan dalam menentukan sama ada fungsi semakin meningkat atau menurun dengan sewajarnya. Ini adalah demonstrasi yang jelas bagaimana kedua -dua konsep itu digunakan dalam kehidupan individu.

4) Kelajuan dan fungsi pembezaan dan integrasi

Perbezaan lain antara integrasi dan pembezaan adalah peranan yang mereka mainkan ketika datang ke mana -mana fungsi tertentu yang disiasat. Menurut ahli matematik, pembezaan dengan ketara membantu menentukan kelajuan fungsi dengan membantu dalam pengiraan halaju seketika. Sebaliknya, integrasi berkenaan dengan menentukan yang dikeluarkan oleh mana -mana fungsi tertentu. Kawasan di bawah lengkung dianggarkan bersamaan dengan jarak yang dilalui oleh fungsi. Ekspresi algebra integrasi membantu dalam mengira kawasan di bawah lengkung, yang berjumlah jarak yang dilalui oleh fungsi.

Ekspresi/Formula Algebra untuk Pembezaan dan Integrasi

Perlu diingat bahawa pembezaan dan integrasi mempunyai ungkapan algebra yang berbeza, yang digunakan dalam pengiraan. Ini menjelaskan mengapa kedua -dua konsep kalkulus akan sentiasa memberikan hasil yang berbeza.  Derivatif fungsi f (x) mengenai pembolehubah x dan mengikut peraturan produk akan ditakrifkan sebagai:

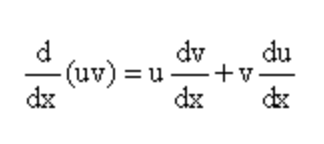
Sebaliknya, formula integrasi atau kawasan integral di bawah lengkung boleh dikira dengan menggunakan formula:

∫f (x) dx, yang merupakan formula yang diterima pakai di bawah kaedah penggantian.

5) Tambahan dan Bahagian

Kaedah lain untuk membandingkan integrasi kepada pembezaan adalah secara khusus menjelaskan bagaimana setiap fungsi menyedari hasilnya. Integrasi menentukan hasil fungsi tertentu dengan menambahkan aspek yang berkaitan dengan pengiraan. Sebaliknya, pembezaan menentukan halaju seketika dan kelajuan fungsi melalui pembahagian.

Perbezaan antara pembezaan dan integrasi: carta perbandingan

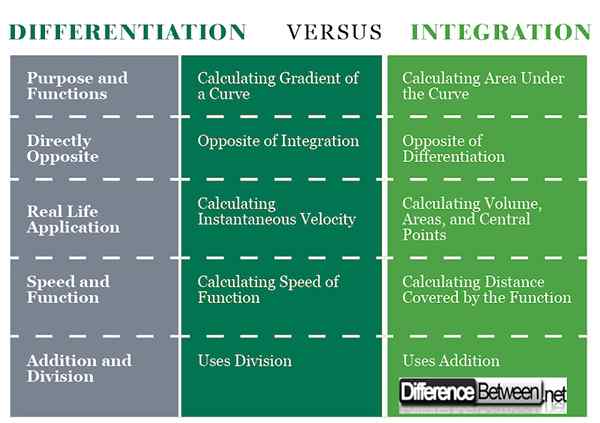
Ringkasan Pembezaan vs. Integrasi

• Salah satu variasi utama antara pembezaan dan integrasi adalah bahawa kedua -dua fungsi kalkulus bertentangan dengan satu sama lain dalam aplikasi mereka.
• Pelajar dan ulama lain harus memberi tumpuan kepada pemahaman salah satu konsep yang kemudiannya dikehendaki untuk melakukan yang bertentangan untuk menentukan hasil fungsi lain.
• Memahami perbezaan yang wujud antara integrasi dan pembezaan adalah penting kerana ia akan membantu individu menggunakan ungkapan algebra yang tepat di mana perlu.
• Akhir sekali, adalah penting untuk menguasai dua konsep kalkulus dalam matematik asas kerana mereka secara konsisten telah digunakan dalam pelbagai bidang seperti ekonomi, perniagaan, dan kejuruteraan.